خلاصه‌ای از بخش‌های کتاب

اعداد اول و فرضیه ریمان

بَری مِی‌زِر، ویلیام اِستاین

ترجمه کامران بزرگزاد ایمانی

مقدمه مترجم. 3

درباره کتاب.. 3

اهمیت ترویج دانش ریاضی.. 4

کتاب مورد استفاده چه کسانی است؟. 6

درباره نویسند‌گان.. 7

مقدمه مؤلفین. 9

فصل 1. 16

نظرات قدیمی، قرون وسطایی، و جدید درمورد اعداد. 16

فصل 2. 20

یک عدد اول چیست؟. 20

فصل 3. 27

اعداد اولِ معروف.. 27

مقدمه مترجم

درباره کتاب

بی‌تردید فرضیه ریمان مهمترین مسئله حل نشده در ریاضیات معاصر است. هنگامی که برنهارت ریمان طی مقاله مشهوری که در سال 1859 منتشر کرد، این فرضیه را مطرح نمود، نه خودش، و نه هیچ کس دیگری تصور نمی‌کرد که اثبات آن اینقدر سخت باشد. خیلی از مسائل دیگر، که مشهورترین آنها آخرین قضیه فِرما است، با وجود اینکه ظاهراً سخت‌تر بنظر می‌رسیدند و ریاضیدانان تصور می‌کردند ممکن است اثبات آنها بیشتر بطول بی‌انجامد، در طول قرن بیستم حل شدند[1]. ولی با اینحال فرضیه ریمان هنوز از خودش مقاومت نشان می‌دهد. در فصول آخر این کتاب حدس زده می‌شود که دلیل این موضوع این است که در پس فرضیه ریمان اصول بنیادی‌تری قرار دارد که باید مشخص شوند، و پس از اینکه این اصول مشخص شدند، فرضیه ریمان خود به خود حل خواهد شد. و همینجا است که اهمیت فرضیه ریمان مشخص می‌شود؛ فرضیه‌ای که با اساسی‌ترین عناصر ریاضیات، مثل سرشتِ اعداد، گره خورده. اینکه گفته می‌شود باید تکلیف موضوعاتی روشن شود که اساسی‌تر هستند، در همین است. ولی آیا چیزهایی هستند که از اعداد بنیادی‌تر باشند، و ما هنوز درک روشنی از آنها نداریم؟ پاسخ این سئوال معلوم نیست و ریاضیدانان در تلاشند تا آنها را توضیح دهند.

اگر فرضیه ریمان حل شود، حقیقتاً انقلاب بزرگی در ریاضیات، و بالطبع در بقیه علوم، رخ خواهد داد، زیرا این فرضیه به موارد شناخته‌شده و ناشناخته زیادی، از جمله ماهیت اعداد و چیز‌هایی که ممکن است در فرای آنها وجود داشته باشند، گره خورده. این نظریه‌ ناشناخته  که ریاضیدانان به دنبال آن هستند، شبیه ”نظریه همه‌ چیز[2]“ در فیزیک خواهد بود که فیزیکدانان دهه‌ها است در جستجوی آن هستند، و اگر پیدا شود، نظریه‌ای خواهد بود که می‌تواند حوزه‌های اصلی فیزیک را به هم پیوند دهد. موضوعات  مختلف مرتبط با فرضیه ریمان، کلاً تحت عنوان ”فرضیه بزرگ ریمان“، یا ” فرضیه ریمان گسترش یافته “ طبقه بندی می‌شود و پیشرفت‌هایی هم در آن حاصل شده.

در این کتاب بارها از اصطلاح «پلکان اعداد اول» استفاده شده که برگرفته از کتاب موسیقی اعداد اول، نوشته مارکوس دو ساتوی است. برای رفع ابهام باید اشاره کنم که ”پلکان اعداد اول“ به تابع شمارنده اعداد اول، یا π(x)، دلالت دارد، که از لحاظ فنی یک تابع پله‌ای است، و به همین جهت از نمودار آن تحت عنوان ”پلکان اعداد اول“ نام برده شده.

این دومین کتابی است که درباره فرضیه ریمان و اعداد اول ترجمه می‌کنم. کتاب قبلی ”دغدغه اعداد اول“ نوشته جان داربی‌شِر بود که نویسندگان کتاب حاضر نیز چندین بار به آن ارجاع می‌دهند. برخی ممکن است بپرسند که آیا همان کتاب قبلی کافی نبود؟ پاسخ این است که درباره موضوع به این مهمی، انتشار یک کتاب اصلاً کافی نیست! اگر شما به فهرست کتاب‌های عمومی منتشر شده  درباره موضوعات مربوط به فیزیک و کیهان‌شناسی، مثل انفجار بزرگ، سیاه‌چاله‌ها، یا سفر در زمان، نگاهی بی‌اندازید، خواهید دید که در پنجاه سال گذشته ده‌ها کتاب به زبان فارسی درباره این موضوعات ترجمه و منتشر شده. ولی درباره مسئله‌ای با این قدمت و اهمیت، متاسفانه منابع بسیار اندکی به زبان فارسی وجود دارد. از این رو، مترجم کتاب حاضر سعی کرده تا اندازه بسیار اندکی آن را جبران کند.

اهمیت ترویج دانش ریاضی

خیلی‌ها از ترتیب اهمیت موضوعات درک درستی ندارند و تصور می‌کنند که جبهه‌ها و سرحدادت دانش نوین بر موضوعاتی چون نجوم، کامپیوتر، یا پزشکی قرار دارد. این تصور در ظاهر درست است، ولی دانشی هست که از اینها به مراتب بنیادی‌تر است و پیشرفت در آن باعث دگرگونی‌های اساسی در بقیه علوم می‌شوند. این دانش ریاضیات است!

اصولاً کلیه علومِ بشر ابزارهایی برای ارتقاء درک او از جهان هستند. ولی دو ابزار بنیادی هست که بقیه ابزارهای انسان توسط این دو ساخته می‌شود. یکی از آنها منطق، و دیگری ریاضیات است. خیلی‌ها منطق را شاخه‌ای از ریاضیات می‌دانند، ولی این درست نیست زیرا منطق پایه‌‌ای‌ترین دانش بشر، و ترازی برای  سنجش همه چیزها است. ما مفاهیمی بنیادی‌تر از ”درستی“ و ”نادرستی“ یا ”وجود“ و ”عدم‌وجود“ نداریم. هر چیزی باید درست باشد تا چیز دیگری بر اساس آن بنا شود، و این شامل گزاره‌های ریاضی نیز می‌شود. چیز دروغ یا نادرست، یا متناقض بدرد نمی‌خورد. سنجش همه اینها به حوزه منطق تعلق دارد.

ولی گذشته از منطق، ریاضیات ملموس‌ترین ابزار اساسی بشر است، که اگر گزاره‌های آن (مثلِ فرضیه ریمان) از آزمون‌های منطقی گذر کنند، و درستی آنها اثبات شود، به ابزارهای قوی و خدشه ناپذیری تبدیل خواهند شد که می‌توان از آنها برای ساخت ابزارهای بهتر و ملموس‌تر در علوم دیگر استفاده کرد.

خیلی از جوانانی که به کیهان‌شناسی و موضوعات مختلف آن، مانند سیاه‌چاله‌ها یا سفر در زمان علاقه دارند، ممکن است ندانند که اگر کار‌های شخصیت اصلی این کتاب، یعنی عالیجناب برنهارت ریمان نبود، حوزه‌ای بنام حساب تانسوری بنا نمی‌شد، تا 50 سال بعد کسی مثل آلبرت اینشتین پیدا شود و نظریه نسبیت عام را بر اساس آن پایه‌گذاری کند. بدون داشتن ابزاری مثل تانسورها، هیچ یک از موضوعات وابسته به کیهان‌شناسی نوین ممکن نبودند.

کامپیوتر نیز حوزه‌ دیگری است که با ریاضیات وابستگی تنگاتنگی دارد. همه می‌دانند که لغت ”کامپیوتر“ یعنی ”حسابگر“، یعنی چیزی که حساب می‌کند و با اعداد سر و کار دارد. از حدود 80 سال قبل که کامپیوترهای الکترونیکی اختراع شدند، تا به امروز هیچ چیزی تغییر نکرده و کارِ کامپیوترها هنوز حساب کردن است، ولی در دامنه وسیعتر و با سرعت بیشتر. حتی حوزه‌ هوش مصنوعی که به تازگی در اخبار سر و صدای زیادی به پا کرده، در واقع چیز جدیدی نیست و اصول آن به 70 سال قبل و کارهای آلن تورینگ بازمی‌گردد. در اینجا نیز داده‌های کلان با سرعت زیاد مورد پردازش قرار می‌گیرند[3]، ولی این پردازش‌ها نیز چیزی جز محاسبه با اعداد نیستند. هر چه بر قدرتِ پردازش اطلاعات افزوده شود (که به زبان فنی به آن بالا بردن قدرتِ محاسبه گفته می‌شود)، نمودِ هوش مصنوعی نیز بالاتر می‌رود، و باهوش‌تر بنظر می‌رسد. یکی از تکنیک‌های موثر در اینکار، استفاده موثر از الگوریتم‌ها است، که اساساً بر پایه ریاضی قرار دارند. کسانی که با مبانی علم کامپیوتر آشنا باشند، می‌دانند که ریاضیاتِ گسسته و نظریه اعداد در توسعه الگوریتم‌ها سهم اساسی دارند.

کسانی که با زیست‌شناسی نوین، یا زیست‌شناسی ملکولی آشنا باشند می‌دانند که یکی از حوزه‌های نویدبخشی که در چند دهه اخیر ظهور کرده، زیست‌شناسی محاسباتی[4] است، که بطور وضوح با اعداد و ریاضیات سر و کار دارد، و کارشناسان آن، علاوه بر زیست‌شناسی، باید از دانش ریاضی قابل‌ملاحظه‌ای برخوردار باشند. این حوزه می‌تواند پایه‌ای برای پزشکی فوق‌پیشرفته باشد.

کتاب مورد استفاده چه کسانی است؟

نسبت به کتاب قبلی که درباره فرضیه ریمان ترجمه کردم، یعنی کتاب ” دغدغه اعداد اول “، کتاب حاضر پیشرفته‌تر محسوب می‌شود، زیرا در آن به موارد ریاضی بیشتری اشاره شده. تفاوت دیگر آن با کتاب قبلی  این است که کتاب حاضر توسط دو ریاضیدان حرفه‌ای یعنی، بَری مِی‌زِر، و ویلیام اِستاین نوشته شده که هر کدام در حوزه کاری خود استادان شناخته‌شده‌ای هستند. بری مِی‌زِر یکی از ریاضیدانان تراز-اول جهان است که در بسیاری از حوزه‌ها کار کرده، و ویلیام اِستاین هم ریاضیدانی است که تخصص اصلی او روی حوزه ریاضیات محاسباتی و جبر کامپیوتری است، که در نیم قرن اخیر در تکامل فرضیه ریمان کاربردهای فراوانی پیدا کرده‌اند.

کتاب کلاً به چهار بخش تقسیم شده که بخش اول آن را ، که تقریباً نیمی از کتاب را تشکیل می‌دهد، می‌توان با داشتن معلوماتی در حد ریاضیات دبیرستانی و دروس اولیه دانشگاهی مطالعه کرد. بخش‌ دوم و سوم کتاب بر استفاده از آنالیز فوریه[5] در تحلیل فرضیه ریمان تکیه دارد، که دانشجویان رشته‌های ریاضی و فنی مهندسی که با این ابزار مهم آشنایی دارند می‌توانند آن را مطالعه کنند. بخش چهارم نیز به استفاده از آنالیز مختلط و نظریه تحلیلی اعداد  اختصاص دارد که دانشجویان رشته ریاضی با آنها بهتر آشنا هستند.

در این کتاب هیچ اشاره‌ای به زمینه‌های تاریخی که در پشت فرضیه ریمان قرار دارد نشده، و تقریباً یک کتاب فنی است، البته نه آنقدر فنی که کسانی که به ریاضیات علاقه دارند نتوانند آن را مطالعه کنند. در صورتی که شما می‌خواهید با جنبه‌های تاریخی و مقدماتی این موضوع  آشنا شوید، می‌توانید در کنار کتاب حاضر، کتاب دغدغه اعداد اول، نوشته جان داربی‌شر را نیز مطالعه کنید.

درباره نویسند‌گان

 بَری مِی‌زِر (Barry Mazur) ریاضیدان پیش‌کسوت آمریکایی است. او در سال 1937 در نیویورک بدنیا آمد، در دانشگاه‌های ام.آی.تی و پرینستون درس خواند، و علاوه بر دانشگاه‌های مختلف آمریکا، فعلاً در دانشگاه هاروارد تدریس می‌کند. او یکی از ریاضیدانان برتر آمریکا و جهان محسوب می‌شود، که سهم مهمی در توسعه ریاضیاتِ نوین و پرورش ریاضیدانان معاصر دارد. از حوزه‌های کاری او می‌توان به نظریه اعداد، هندسه دیوفانتی، مانیفُلدهای مِی‌زِر، تابع زتای آرتین- مِی‌زِر، .... اشاره کرد.

ویلیام اِستاین (William Stein) ریاضیدان و برنامه‌نویس آمریکایی است. او در سال 1974 در کالیفرنیا بدنیا آمد. در دانشگاه واشینگتن درس خواند و فعلاً هم در همین دانشگاه تدریس می‌کند.

به دلیل علاقه‌ای که اِستاین به حوزه ریاضیات محاسباتی دارد، در کارهای خودش از کامپیوتر استفاده فراوانی می‌کند، و از سال 2005 تاکنون مشغول توسعه نرم‌افزاری بنام SageMath بوده که در حوزه سیستم‌های جبر کامپیوتری (CAS) یکی از برنامه‌های مطرح است، و برخلاف نرم‌افزارهای تجاریِ مشابه، مانند Mathematica و Maple، رایگان است.

 برای رسم نمودارهای این کتاب و برخی محاسبات وابسته، از همین نرم‌افزار استفاده شده.

تابستان 1402

                  کامران بزرگزاد

مقدمه مؤلفین

فرضیه ریمان (Riemann Hypothesis) یکی از مسائل مهمِ حل نشده در ریاضیات است و جایزه یک میلیون دلاری موسسه ریاضی کلِی (Clay) در انتظار کسی است که آن را حل کند. ولی حل آن (چه با جایزه و چه بدون جایزه) برای درک ما نسبت به ماهیت اعداد بسیار مهم است.

اخیراً چندین کتاب کامل برای مخاطبین عام نوشته شده که موضوع اصلی آنها فرضیه ریمان است[6]. این کتاب‌ها تصویر نسبتاً پرباری از شخصیت‌های درگیر در فرضیه ریمان و مسائل ریاضی و تاریخی مرتبط به آن ارائه می‌دهند.

ولی هدف کتاب حاضر این نیست. در عوض، هدف ما این است که تا جایی که ممکن است، مستقیماً و با کمترین زمینه ریاضی، توضیح دهیم که فرضیه ریمان چیست و چرا اینقدر مهم است. زیرا حتی قبل از اینکه کسی درستی (یا نادرستی) این فرضیه را ثابت کند، آشنایی با آن، و برخی ایده‌هایی که پشت آن قرار دارند، بسیار هیجان‌انگیز است. علاوه‌براین، این فرضیه در طیف وسیعی از حوزه‌های ریاضی از اهمیت حیاتی برخوردار است. به عنوان مثال، حتی اگر فرضیه ریمان هرگز اثبات نشود، با فرض صحت آن (و فرضیه‌هایی که بطور نزدیک با آن رابطه دارند) این فرضیه در مسائل مربوط به ریاضیات محاسباتی، اعتماد به نفس ما را تقویت می‌کند، بصورتی که درک بسیار خوبی از مدت زمان اجرای برنامه‌های خاص کامپیوتری به ما می‌دهد، و در برخی موارد به ما اطمینان خاطر می‌دهد که می‌توانیم محاسباتی را انجام دهیم که ممکن است هفته‌ها یا حتی ماه‌ها طول بکشد، محاسباتی که نهایتاً به جواب منتهی خواهند شد.

شکل 1: پیتر سارناک (Peter Sarnak).

پیتر سارناک (Peter Sarnak)، استاد دانشگاه پرینستون تاثیر گسترده فرضیه ریمان را چنین توصیف می‌کند:

«فرضیه ریمان یک مسئله اساسی است، و بر چیزهای بسیار زیادی دلالت دارد. چیزی که باعث می‌شود این فرضیه در ریاضیات تا حدی غیرمعمول بنظر برسد این است که بیش از پانصد مقاله (یا شاید هم بیشتر) وجود دارند که با عبارت زیر شروع می‌شوند:

”با فرض اینکه فرضیه ریمان درست باشد[7] ...“،

 و نتیجه‌گیری‌هایی که بر اساس همین فرض ساده صورت می‌گیرد فوق العاده هستند. و پس از آن، این نتیجه‌گیری‌ها به قضایای مختلف تبدیل می‌شوند ... و با همین فرض ساده، شما به یکباره پانصد قضیه (یا شاید هم بیشتر) را ثابت ‌کرده‌اید.»

خوب این فرضیه ریمان چیست؟ در زیر اولین توضیحی که در مورد آن هست را می‌آوریم. هدف کتاب ما این است که توضیح کامل‌تری از این فرضیه ارائه دهیم و شما را  از اهمیت این مسئله، و ریاضیاتِ زیبایی که در پشت آن نهفته شده آگاه کنیم. ما در طول این کتاب برای فرمولبندی دقیق این فرضیه چند روش متفاوت (اما معادل)  ارائه خواهیم داد، که در کادرهای چهارگوش نمایش داده می‌شوند. منظور ما از اینکه دو گزاره ریاضی «معادل» هم هستند این است که با توجه به وضع فعلی دانشِ ریاضی ما، این امکان وجود دارد که ثابت کنیم اگر یکی از آن گزاره‌ها درست باشد، دیگری هم درست است.

شکل 2: رائول بات (2005-1923).

ریاضیدان مجار-تبار آمریکایی، رائول بوت (Raoul Bott)، در توصیه به یکی از شاگردانش یکبار گفته بود ”اگر کسی یک کتاب یا مقاله ریاضی را می‌خواند، یا در یک کنفرانس ریاضی شرکت می‌کند، باید هدفش این باشد که با چیز بسیار مشخصی به خانه برگردد، این چیز می‌تواند کوچک باشد، ولی باید مشخص باشد. چیزی که در دسته وسیعتری از مسائل ریاضی کاربردهایی داشته باشد، کاربردهایی که نسبت به آنچه در کتاب یا سخنرانی آمده گسترده‌تر باشند. اگر بخواهیم برخی از این مواردِ مشخص را در مورد این کتاب مثال بیاوریم، می‌توانیم از سه عبارتِ کلیدی اعداد اول، دقتِ جذری ، و طیف نام ببریم. به منظور اینکه شما را تشویق کنیم تا در اولین مورد این فهرست، یعنی اعداد اول، فکر کنید، هیچ چیز بهتر از این نیست  که قسمتی از مقاله 12-صفحه‌ای ”50 میلیون عدد اول“، نوشته دون زاگیر (Don Zagier) را نقل کنیم:

شکل 3: دون زاگیر (-1951).

”دو واقعیت مهم در مورد توزیع اعداد اول وجود دارد، که امیدوارم بتوانم شما را چنان متقاعد کنم که برای همیشه در ذهن‌تان حک شوند. اولین مورد این است که [آنها] تصادفی‌ترین و بدقلق‌ترین اشیایی هستند که توسط ریاضیدانان مورد مطالعه قرار گرفته‌اند: آنها مانند علف‌های هرز در میان اعداد طبیعی رشد می‌کنند، طوری که به نظر می‌رسد آنها از قانون دیگری جز قانون شانس پیروی نمی‌کنند، و هیچ کس نمی‌تواند پیش‌بینی کند که سر و کله عددِ [اولِ] بعدی کجا پیدا می‌شود. واقعیت دوم، که حتی از این هم شگفت‌انگیزتر است، دقیقاً عکس مورد قبل را بیان می‌کند، یعنی می‌گوید: اعداد اول نظم خیره‌کننده‌ای از خودشان نشان می‌دهند، قوانینی بر رفتار آنها حاکم است، و آنها با دقت بسیار از این قوانین پیروی می‌کنند.“

ریاضیات در حال شکوفایی است. هر سال شاهد ابتکارات جدید و هیجان‌انگیزی هستیم که کاربردهای فرضیه ریمان را گسترش داده و آن را مشخص‌تر می‌کند، و مسیرهای جدیدی برای کاوشِ عمیق (و درک دقیق‌تر) در حوزه‌های ریاضیات کلاسیک (و جدید) برای ما فراهم می‌آورد. در مسیر چنین اکتشافاتی، ما ابزارهای بیشتر و قدرتمندتری را برای خودمان ایجاد می‌کنیم. ما راه حل‌ سؤالات مهم را می‌بینیم. ولی با این حال در دیدگاه خودمان با شگفتی‌ و تغییرات چشمگیر مواجه می‌شویم.

مجموعه‌ای از تکنیک‌های شگفت‌انگیز به ریاضیدانان اجازه می‌دهد کار خود را انجام دهند: چارچوب‌بندی تعاریف، تولید سازه‌ها، فرمول بندی قیاس‌هایی که مفاهیمِ متفاوت و زمینه‌های ریاضی متفاوت را به هم مرتبط می‌کنند. ایجاد حدس و گمان، که راه‌های ممکن را شکل می‌دهد؛ و مهمتر از همه، اساس کار که عبارت است از ارائه اثبات‌های غیرقابل تردید از آنچه مطرح شده. ایده انجام چنین کارهایی، خودش یکی از افتخارات بزرگ ریاضیات است.

در این میان  نظریه اعداد سهم خودش را دارد. در کنار تمام کارهای نظری، یکی از چیزهایی که نظریه اعداد ارائه می‌دهد، لذت ناب محاسبات عددی است، که (وقتی خوب پیش می‌رود) به شما امکان می‌دهد تا  (عیناً) شاهد پیچیدگی اعداد و روابط عمیقی باشید که نیاز به توضیح دارند. شگفت آور است که هر چقدر هم که شما اطلاع زیادی از نظریه اعداد نداشته باشید، بااینحال نمی‌توانید از آنچه کاوش‌های عددی از خودشان نشان می‌دهند لذت نبرید.

این کتاب قرار است سرآغازی برای این لذت‌ها باشد. ما نسبت به اساس بحث خودمان یک رویکرد تجربی داریم که به کمک محاسبات عددی و نمودارها نمایش داده می‌شوند. در نتیجه، کتاب ما پر از تصاویر و نمودار است[8].

تعداد اندکی از معادلات ریاضی در بخش اول کتاب وجود دارد. این بخش برای خوانندگانی است که عموماً به ایده‌های ریاضی علاقه دارند یا در مورد آنها کنجکاو هستند، اما ممکن است هیچ موضوع پیشرفته‌ای را مطالعه نکرده باشند. بخش اول به توضیح ماهیت فرضیه ریمان و اهمیت آن، و اینکه چرا ریاضیدانان آنقدر به آن علاقه دارند اختصاص دارد. مطالعه این بخش به دانش ریاضی زیادی نیاز ندارد، و مثلاً از حساب دیفرانسیل و انتگرال استفاده نمی‌کند، هر چند دانستن مفهومِ تابع مفید است. به دلیل اینکه قسمت اول کتاب دارای بخش‌های مقدمه، میانی، و موخره است، کامل محسوب می‌شود. امیدواریم خوانندگانی که فقط قسمت اول را می‌خوانند از هیجان این موضوع مهم ریاضی لذت ببرند.

بخش دوم کتاب برای خوانندگانی است که حداقل یک دوره حساب دیفرانسیل و انتگرال را گذرانده‌اند. این بخش نوعی آماده سازی برای ورود به مبحث آنالیزِ فوریه (Fourier analysis) است که در قسمت‌های بعدی خواهد آمد. مفهوم اصلی که در این بخش مورد بررسی قرار می‌گیرد، مفهوم طیف (spectrum) است.

بخش سوم برای خوانندگانی است که مایلند به طور واضح‌تر رابطه‌ای که بین موقعیت اعداد اول و آنچه ماطیفِ ریمان[9] می‌نامیم را ببینند.

بخش چهارم نیاز به آشنایی با توابع تحلیلی مختلط دارد و به دیدگاه اصلی ریمان باز می‌گردد. این بخش «طیفِ ریمان»، که در بخش سوم مورد بحث قرار خواهد گرفت، را به صفرهای بی‌اهمیت تابع زتای ریمان مرتبط می‌کند. ما همچنین بطور کوتاه برخی از نسخه‌های مختلفی که برای فرضیه ریمان ارائه شده را توضیح می‌دهیم.

یادداشت‌های پایانی که در برخی قسمت‌ها آمده برای پیوند دادن متن به منابع است، ولی آنها همچنین برای ارائه توضیحات فنی بیشتر درمورد زمینه‌های ریاضی فصل‌های بعدی نیز کاربرد دارند. ارجاع به یادداشت‌های پایانی در داخل پرانتز خواهد بود[10].

فصل 1

نظرات قدیمی، قرون وسطایی، و جدید درمورد اعداد

اگر بخواهیم حرف فیلسوفِ یونانِ باستان، یعنی ارسطو، را بپذیریم، فیثاغورثیانِ[11] باستان عقیده داشتند که اصول حاکم بر اعداد، «اصولی است که بر همه چیز حاکم است» ، مفهوم عدد اساسی تر از خاک، هوا، آتش، یا آب است، که طبق عقاید یونانیان باستان، چهار جزء سازنده ماده بودند. اندیشیدن درمورد اعداد یعنی نزدیک شدن به معماری «هستی».

در اینصورت، ما از لحاظ فکری چقدر با  اعداد نزدیکی داریم؟

شکل 1.1: رنه  دکارت (1650-1596).

تقریباً چهار قرن پیش فیلسوف و ریاضیدان فرانسوی، رنه دکارت (Rene Descartes) ابراز امیدواری کرد که به زودی در هندسه «تقریباً هیچ چیز دیگری برای کشف کردن وجود نداشته باشد». فیزیکدانان معاصر نیز رویای یک نظریه نهایی را در سر می‌پرورانند.[12] اما ریاضیاتِ محضِ اعداد، علیرغم تقدس، قدرت، و زیبایی که دارد، ممکن است هنوز در مراحل اولیه توسعه خود باشد و مانند روح انسان، اعماق آن بی‌پایان باشد، و هیچ وقت یک نظریه نهایی برای آن یافت نشود.

شکل 1.2: ژان دو بوشر، «دون کیشوت و دولسینیا دل توبوسو» از کتاب تاریخ دون کیشوت دو لامانچا، اثر میگل د سروانتس. انتشارات ترانس. توماس شلتون جورج اچ دوران، نیویورک (1923).

هنگامی‌که دون کیشوت از شاعری خواست تا برای بانویش «دولسینیا دل توبوسو» شعری بسازد که حرف اول هر سطر به ترتیب با یکی از حروف نام او آغاز شود، شاعر اینطور جواب داد:

” اعداد چیزهای بدقلقی هستند. در ترکیب نام او مشکل بزرگی وجود دارد زیرا تعداد حروف نام او 17 عدد است و اگر او چهار مصرع کاستیلی بسازد که از چهار سطرِ هشت هجایی تشکیل شده است، یک حرف زیادی خواهد بود و اگر مصرع‌های پنج سطری هشت هجایی بسازد، آنهایی که d'ecimas یا ردوندیلا نامیده می‌شوند، بازهم سه حرف کم خواهند بود...“

دون کیشوت که حاضر نبود سرسختی و تقسیم‌ناپذیری عدد 17 را بپذیرد، به شاعر التماس کرد و گفت ”ولی باید راهی برای اینکار باشد ...“

در واقع هفده یک عدد اول است، که این یعنی هیچ راهی برای تجزیه آن به حاصلضرب‌ اعداد کوچکتر وجود ندارد، و به همین دلیل هم هست که این عدد در برخی از پدیده‌های طبیعی ظاهر می‌شود. مثلاً هفده سال طول می‌کشد تا سر و کله برخی از زنجره‌ها (Cicadas) در مزارع و دره‌ها پیدا شود.

شکل 1.3: زنجره‌هایی که هر 17 سال یک بار تولید مثل می‌کند.

علیرغم جایگاه ویژه اعداد اول در درکِ نوین ما از اعداد، آنها در ادبیات باستانی پیش از اقلیدس (حداقل در ادبیات مکتوب آن زمان) خیلی مورد توجه قرار نگرفتند. در نوشته‌های یکی از فیلسوفان پیش از افلاطون بنام فیولائوس (Philolaus)، از اعدادِ اول به عنوان دسته‌ای از اعداد نام برده شده. با اینکه افلاطون علاقه شدیدی به ریاضیات داشت، ولی در گفتگوهای موسوم به افلاطونی، از آنها به طور خاص صحبت نشده، که این تعجب برانگیز است. ولی آنها بطور گاه به ‌گاه در نوشته‌های ارسطو ظاهر می‌شوند، که با توجه به تأکید ارسطو بر تمایز بین مرکب و ساده، جای تعجب ندارد. ارسطو در جلدِ 13 کتاب متافیزیک می‌گوید: «ساده بر مرکب مقدم است».

ولی جایی که در ابتدا اعداد اول به طور جدی مطرح شدند، در کتاب اصول اقلیدس بود!

شکل 1.4: اقلیدس

حقایق ثابت شده زیادی در مورد اعدادِ صحیح وجود دارد. این حقایق موجب می‌شوند تا بر هیبت و پیچیدگی زیبایِ اعداد اول اضافه شود. اما هر یک از اکتشافات جدید و مهمی‌که درباره آنها انجام می‌دهیم، سؤالات، حدس‌های قریب به یقین، اکتشافات، انتظارات، و مشکلات حل‌نشده بیشتری را به همراه داردند.

فصل 2

یک عدد اول چیست؟

اعداد اول نیز مانند اتم‌ها‌ تجزیه ناپذیر هستند. برای اینکه از ابتدا شروع کنیم، عمل ضرب را به عنوان پیوندی در نظر بگیرید که اعداد را به هم متصل می‌کند. مثلاً معادله 2×3=6  موجب می‌شود تا عدد 6 را مانند مولکولی تصور کنیم که از اتم‌های کوچکتر، یعنی 2 و 3، تشکیل شده. اگر این روند را معکوس کنیم، یعنی کار را با عدد صحیحی مثل 6 شروع کنیم، در آن صورت ممکن است بخواهیم آن را تجزیه کنیم (یعنی آن را به شکلِ حاصل ضرب اعداد صحیح کوچکتر بیان کنیم) و البته نهایتاً به این نتیجه برسید که 6=2×3، و کشف کنید که عوامل اول 6 فقط 2 و 3 هستند. بنابراین، اعداد 2 و 3 موجودات تجزیه ناپذیر، یا همان اتم‌هایی هستند که عدد ما (یعنی 6) را تشکیل می‌دهند.

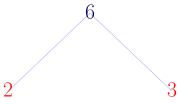
شکل 2.1: عدد 6 برابر است با 2 × 3

طبق تعریف، یک عدد اول  یک عدد صحیح بزرگتر از  1 است، که نمی‌توان آن را بصورت حاصل ضرب دو عدد صحیح کوچکتر تجزیه کرد. بنابراین،2  و 3 دو عدد اول هستند. بعد از 2  و 3، عدد بعدی که در امتداد خط اعداد صحیح قرار دارد، 4 است، که اول نیست، زیرا 4=2×2. ولی عدد بعدی، یعنی 5، اول است. از لحاظ ضربی، اعداد اول اجزاء سازنده اعداد هستند، بصورتی که می‌توان همه اعداد را از آنها ساخت. در حساب یک قضیه اساسی هست که به ما می‌گوید هر عدد (بزرگتر از 1) را می‌توان به حاصل ضرب اعداد اول تجزیه کرد، و به غیر از اینکه بخواهیم جای اعداد اول را تغییر دهیم، این تجزیه یکتا  است.

برای مثال، اگر شما بخواهید عدد 12 را به شکل ضرب دو عدد کوچکتر بیان کنید، صرف نظر از  ترتیب نوشتن آنها، به دو صورت می‌توان اینکار را انجام داد:

12 = 2 × 6 و         12 = 3 × 4

ولی هیچکدام از اینها تجزیه کامل 12 نیستند، زیرا نه 6 و نه 4 اول نیستند، و بنابراین می‌توانند تجزیه شوند. پس با تغییرِ ترتیبِ نوشتن آنها از کوچک به بزرگ، ما می‌توانیم 12 را به صورت زیر بنویسیم:

12 = 2 × 2 × 3

اگر شما تلاش کنید عدد 300 را تجزیه کنید، از طرق زیای می‌توانید اینکار را انجام دهید:

300 = 30 × 10 یا   300 = 6 × 50

و خیلی راه‌های دیگر. ولی اگر شما کار تجزیه هر یک از این اعداد را ادامه دهید، و از آنها یک درخت تجزیه بسازید، در تَه این درخت به تجزیه یکسانی خواهید رسید که در شکل 2.2 نشان داده شده است:

300 = 2² × 3 × 5².

شکل 2.2: دو درخت تجزیه که نشان دهنده تجزیه عدد 300 به حاصل ضرب اعداد اول هستند.

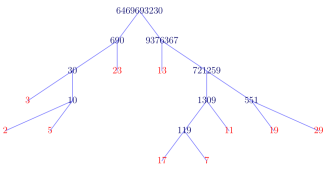
شکل 2.3: درخت تجزیه برای عدد 6469693230.

فرضیه ریمان این سؤال را بررسی می‌کند که ” ما چقدر می‌توانیم اعداد اول، یعنی همان اتم‌های تشکیل دهنده ضرب، را بشناسیم؟" اعداد اول بخش مهمی‌از زندگی روزمره ما هستند. به عنوان مثال، اغلب ما وقتی از یک وب سایت بازدید می‌کنیم و چیزی را بصورت آنلاین می‌خریم، برای خصوصی نگه داشتن تراکنش‌های بانکی ما، از اعداد اولی استفاده می‌شود که صدها رقم اعشاری دارند. این استفاده همه جانبه از اعدادِ اولِ بسیار بزرگ، به یک اصل بسیار ساده تکیه دارد، که ضرب اعداد در یکدیگر، از تجزیه آنها بسیار ساده‌تر است. مثلاً اگر عدد  391 را در نظر بگیرید، قبل از اینکه متوجه شوید 391=17×23، ممکن بود برای مشخص شدن این نتیجه، چند دقیقه سر خود را بخارانید. اما اگر قرار بود 17  را در 23  ضرب کنید، بلافاصله می‌توانید این کار را انجام ‌دهید. دو عدد اول، مثل P و Q  را در نظر بگیرید که هر کدام چند صد رقم دارند، و آنها را به یک کامپیوتر ساده وارد کرده و از آن بخواهید که این دو عدد را در هم ضرب کند: شما ظرف حدود یک هزارم‌ثانیه حاصل ضرب N=P×Q که صدها رقم دارد، را دریافت خواهید کرد. اما اگر عدد N را به هر کامپیوتر رومیزی بدهید و از آن بخواهید N را تجزیه کند، این کامپیوتر (به احتمال زیاد) در انجام چنین کاری شکست خواهد خورد.

ایمنی بسیاری از رمزگذاری‌ها به دشواری تجزیه اعداد، و به همین « شکستِ تضمین شده» بستگی دارد[13]!

اگر شما جزء متخصصین اعداد بودید، ممکن بود از کشف و اثبات اینکه عدد زیر

یک عدد اول است و 12,978,189 رقم دارد، لذت ببرید! این عدد اول، که در 23 آگوست سال 2008 توسط پروژه GIMPS[14] یافت شد. گرچه این عدد بزرگترین عدد اول شناخته شده نیست، ولی اولین عدد اول کشف شده‌ است که بیش از ده میلیون رقم دارد.

عدد2^43,112,609-1 حقیقتاً عدد بزرگی است! فرض کنید کسی به شما بگوید که ”مطمئناً p=2^43,112,609-1  بزرگترین عدد اول است!“ (که البته اینطور نیست). در اینصورت شما بدون اینکه صریحاً عدد اول بزرگتری را برای او مثال بیاورید، چگونه می‌خواید او را قانع کنید که اشتباه می‌کند؟

لُب کلام این است که نشان دهیم اعداد اول دیگری نیز وجود دارند که از p=2^43,112,609-1  بزرگترند. فرض کنید عدد بزرگی بنام M را تشکیل دهیم. عدد M حاصل ضرب کلیه اعداد اول، تا p=2^43,112,609-1 در خودشان است که البته شامل خود p هم می‌شود. حالا عدد 1 را به M اضافه کنید تا عدد N حاصل شود: N=M+1.

حالا هرچند عدد N بسیار بزرگ است، ولی دو احتمال وجود دارد؛ یکی اینکه N یک عدد اول باشد، که یعنی اعداد اولی (مثل N) وجود دارند که حقیقتاً از p=2^43,112,609-1 بزرگترند، و دیگری اینکه N اول نیست و به عدد اولی مانند P بخش‌پذیر است.

واضح است که P از p بزرگتر است، زیرا کلیه اعداد اول کوچکتر یا مساوی p ، عدد M را بخش کرده‌اند، بنابراین این اعداد نمی‌توانند N=M+1 را بخش کنند (زیرا آنها بر M بخش‌پذیر هستند و اگر تلاش کنید N=M+1 را بر هر یک از آنها تقسیم کنید، شما باقیمانده 1 را بدست می‌آورید). بنابراین، چون P عدد N را بخش کرده، این عدد نمی‌تواند هیچ یک از اعداد اول کوچکتر یا مساوی p  باشد. بنابراین P عدد اولی است که از p=2^43,112,609-1  هم بزرگتر است.

ضمناً باید بگوییم که رویکرد مذکور برای اثبات نامحدود بودن اعداد اول، اصلاً رویکرد جدیدی نیست، و در واقع قدمت آن به دو هزار سال قبل بازمی‌گردد، زیرا این استدلال در کتاب اصول اقلیدس آمده بود. یونانی‌ها می‌دانستند تعداد اعداد اول بی‌نهایت است و آنها نیز از همان روشی استفاده می‌کردند که ما برای نشان دادن اینکه p=2^43,112,609-1  بزرگترین عدد اول نیست از آن استفاده کردیم.

بار دیگر این استدلال را بطور خلاصه تکرار می‌کنیم: فرض کنید که اعداد p₁, … p_m  اول باشند، و n=p₁p₂…p_m + 1 . آنگاه n بر هیچ یک از اعداد اول p_i بخش‌پذیر نیست، بنابراین هرچقدر هم m بزرگ باشد، تعداد اعداد اول از m بیشتر است.

شما می‌توانید این رویکرد را شبیه یک بازی ساده در نظر بگیرید که می‌توانید آن را بازی کنید. کار را با کیسه‌ای از اعداد اول شروع کنید که فقط شامل دو عدد اول 2  و 3  است. حالا هر "حرکتِ" بازی شامل ضرب تمام اعداد اولی است که در کیف دارید تا عددی مثل M را بدست آورید، سپس 1 را به M اضافه کنید تا عدد بزرگتر N=M+1 حاصل شود، سپس N را به عوامل اول تجزیه کنید و سپس تمام آن اعداد اول جدیدی که از این تجزیه حاصل شده را در کیسه خود قرار دهید. اثبات اقلیدس به ما نشان می‌دهد که با هر حرکت این بازی، اعداد اول بیشتری پیدا خواهیم کرد، و محتویات کیسه افزایش می‌یابد. مثلاً بعد از یک میلیون حرکت، تضمین می‌شود که کیسه ما بیش از یک میلیون عدد اول داشته باشد.

به عنوان مثال، در ابتدای بازی کیسه فقط حاوی یک عدد اول، یعنی 2، است. در اینجا نحوه رشد کیسه شما با حرکات متوالی بازی نشان داده شده است:

{2}

{2, 3}

{2, 3, 7}

{2, 3, 7, 43}

{2, 3, 7, 43, 13, 139}

{2, 3, 7, 43, 13, 139, 3263443}

{2, 3, 7, 43, 13, 139, 3263443, 547, 607, 1033, 31051}

{2, 3, 7, 43, 13, 139, 3263443, 547, 607, 1033, 31051, 29881, 67003,

9119521, 6212157481}

و غیره[15].

هرچند تعداد اعداد اول بی‌نهایت است، اما یافتن اعداد اول بزرگ بطور صریح، چالش بزرگی است. در دهه 1990، بنیادElectronic Frontier ، به آدرس http://www.eff.org/awards/coop، یک جایزه نقدی 100,000 دلاری به اولین گروهی اختصاص داد که یک عدد اول با حداقل 10,000,000 رقم اعشاری را پیدا کنند (همان گروهی که عدد اول p ذکر شده را در بالا پیدا کردند)، و یک جایزه نقدی 150000 دلاری دیگر را نیز به اولین گروهی خواهد داد که یک عدد اول با حداقل 100،000،000 رقم اعشاری را پیدا کنند.

برای مدتی عدد p=2^43,112,609-1  بزرگترین عدد اول شناخته شده بود، و منظور ما از "شناخته ‌شده" این است که ما به وضوح این عدد را می‌شناسیم، طوری که می‌توانیم محاسباتی را درمورد آن انجام دهیم. برای مثال، ما می‌دانیم که دو رقم آخر p هر دو 1 هستند و مجموع ارقام p برابر با 58416637 است. البته p بزرگترین عدد اول نیست زیرا بی نهایت عدد اول وجود دارد، به عنوان مثال، عدد اولِ بعد از p ، q نام دارد. اما هیچ راه شناخته شده و کارآمدی برای محاسبه چیزهای جالب در مورد q وجود ندارد. مثلاً ما در حال حاضر نمی‌توانیم بگویم که آخرین رقم در بسط اعشاری q چیست؟

فصل 3

اعداد اولِ معروف

اعداد اول انواع مختلفی دارند، برخی از آنها ساده‌تر از بقیه هستند. به عنوان مثال، عددی که در فصل قبل در مورد آن صحبت کردیم، یعنی

p=2^43,112,609-1

به طور چشمگیری شکل خاصی دارد. این عدد، از یکی از توان‌های 2 به‌اندازه یکی کمتر است. تصادفی نیست که بزرگترین عدد اولی که "فعلا شناخته شده" چنین شکلی داشته باشد. دلیلش هم این است که تکنیک‌های خاصی وجود دارد که می‌توانیم از آنها برای بررسی اول بودن اعدادی استفاده کنیم که از توان‌های 2 به‌اندازه یکی کمتر هستند. اعداد اول که چنین شکلی دارند، به اعداد مرسن[16] معروفند، و همچنین اعداد اولی از توان‌های 2 به‌اندازه یکی بیشتر باشند، به اعداد فِرما[17] معروفند.

اگر اولین بار است که با اعداد اولی برخورد می‌کنید که به‌اندازه 1 با توان‌های 2  تفاوت دارند، اینجا دو تمرین وجود دارد که می‌توانید آنها را انجام دهید:

1.        نشان دهید که اگر عددی به شکل M=2ⁿ-1 اول باشد، توان n نیز اول است. [راهنمایی: این معادل اثبات این است که اگر n مرکب است، پس 2ⁿ-1 نیز مرکب است.] برای مثال: 2²-1 =3 ،2³-1= 7  اعداد اول هستند، اما 2⁴-1=15 اول نیست. بنابراین اعداد اول مرسن اعدادی

·         به شکل -1 ^{عدد اول}2 هستند ، و

·         خودشان اعداد اول هستند.

2.       نشان دهید که اگر عددی به شکل F=2ⁿ +1 اول باشد، n توانی از 2 است. به عنوان مثال: 1+2²=5 اول است، اما 1+2³  9=اول نیست. بنابراین اعداد فرما اعدادی هستند که

·         به صورت  +1 ^{توانی از 2}  2 هستند و

·         خودشان اعداد اول هستند.

همه اعدادی که به صورت  -1 ^{عدد اول}  2 یا +1  ^{توانی از 2} 2 هستند اول نیستند. فعلاً ما تعداد محدودی  از آنها را می‌شناسیم که اول هستند. برای اطلاعات بیشتر به آدرس http://www.mersenne.org  رجوع کنید.

...........................................

برای ادامه مطالعه این کتاب نسخه کامل PDF آن را تهیه کنید.