برای روشن‌تر شدن محتوایِ کتابهای ترجمه شده، معمولاً مترجمِ حقیر عادت دارد مقدمه کوتاهی را برای آنها بنویسد. ولی مقدمه این کتاب کمی طولانی‌تر شده. دلیلش هم توضیح مواردی بوده که در مقدمه نویسنده ذکر نشده، یا به خوانند‌گان فارسی زبان ارتباط دارند. بنابراین امیدوارم خواننده محترم پیش از خواندن فصول اصلی کتاب، هم این مقدمه، و هم مقدمه نویسنده را بخواند.

درباره این کتاب

کتاب حاضر بطور اعم درباره اعداد اول، و بطور اخص درباره فرضیه ریمان است. هر کسی که با ریاضیات معاصر آشنا باشد می‌داند که اعداد اول یکی از مفاهیم اساسی در نظریه اعداد هستند. فرضیه ریمان هم موضوع بسیار مهمی است که پیوند تنگاتنگی با اعداد اول دارد، و با اینکه بیش از 150 سال از عمر آن می‌گذرد، هنوز لاینحل باقی مانده. زمانی که برنهارت ریمان در 1859 این فرضیه را مطرح کرد خودش هم تصور نمی‌کرد که چنان اهمیتی پیدا کند. از نظر او، مسئله اصلی چیز دیگری بود و ریمان این فرض را بعنوان یکی از فروعات آن مسئله مطرح کرده بود. ولی او، و هیچ کس دیگری، هنوز نتوانسته این مسئله فرعی را اثبات کند، و از آن زمان به بعد، بعنوان یک فرضیه (Hypothesis) از آن یاد می‌شود.

مسئله اصلیِ مورد نظر، پیدا کردن تابعی برای شمارش اعداد اول بود که از زمان گاوس اهمیت پیدا کرده بود. برای این منظور، ریمان روش‌هایی را ابداع کرد که مخلوطی از علم حساب و آنالیز ریاضی بودند. با تکامل این روش‌ها شاخه جدیدی بوجود آمد که نظریه تحلیلی اعداد نام گرفت، و اکنون یکی از شاخه‌های مهم و فعال ریاضیات محسوب می‌شود.

تلاش مترجم کتاب همیشه بر این بوده تا از میان کتابهای علمی آنهایی را انتخاب کند که موضوعات آنها در حین جالب بودن، تا حدی ساده باشند و طیف وسیعی از خوانندگانی که دانش ریاضی آنها در حد دبیرستان است بتوانند موضوعات مطرح شده را درک کنند. از این جهت من نویسندگانی مثل یان استوارت را انتخاب کردم که از همین سبک و سیاق پیروی می‌کنند. کتاب‌های چرا زیبایی واقعیت است، یا آخرین قضیه فِرما از همین نمونه هستند.

شاید بتوان موضوع این کتاب را با آخرین قضیه فِرما مقایسه کرد. زیرا هر دو آنها درمورد مسائل دشوار ریاضی صحبت می‌کنند که برای مدت طولانی لاینحل باقی مانده‌اند. ولی میان این دو موضوع از لحاظ ظاهری تفاوت عمده‌ای وجود دارد، زیرا صورت مسئله آخرین قضیه فرما بسیار ساده است و هر دانش‌آموز کلاس نهم می‌تواند آن را درک کند:

آخرین قضیه فِرما: معادله $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image001.png$ برای nهای بزرگتر از 2 هیچ جواب صحیحی ندارد.

تقریباً 380 سال طول کشید تا همین مسئله به ظاهر ساده در سال 1994 توسط اندرو وایلز حل شود (برای توضیحات کاملتر به کتاب آخرین قضیه فِرما مراجعه کنید.)

اما توضیح فرضیه ریمان دشوارتر است و نیاز به زمینه‌های ریاضی بیشتری دارد. در اینجا نیز صحبت بر سر یک معادله است، که تابع زتا نامیده می‌شود. فرضیه ریمان درباره تابع زتا اینطور می‌گوید:

فرضیه ریمان:

جواب‌های تابع زتا (که صفرهای آن نیز نامیده می‌شوند)، شامل اعدادِ مختلطی است که بخش حقیقی آنها $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image002.png$ است.

تفاوت عمده‌ای که فرضیه ریمان با آخرین قضیه فرما دارد این است که مسئله فِرما بیشتر به یک مسئله تفننی شباهت داشت، مسئله‌‌ای که صورت آن بسیار ساده بود ولی برای حل آن سلاح‌هایی ابداع شد که چنان پیچیده و پیشرفته بودند که هیچ شباهتی با صورت مسئله اولیه نداشتند. حلِ مسئله فرما اهمیت چندانی ندارد، آنچه اهمیت دارد سلاح‌ها و ابزارهایی است که انگیزه اولیه حل این مسئله بوده‌اند. از آنها می‌توان برای حل بسیاری از مسائل دیگر استفاده کرد.

تفاوت دیگر ”آخرین قضیه فِرما“ و ”فرضیه ریمان“ این است که علاوه بر اینکه ثابت شده فرضیه مذکور بسیار دشوار و سرکش است، همچنین معلوم شده که می‌تواند کاربردهایی در فیزیک نوین، و خصوصاً در فیزیک کوانتوم، داشته باشد. در فصل 18 این کتاب، توضیحاتی در اینباره داده شده.

خواننده ناآشنا با فرضیه ریمان متوجه می‌شود که برای درک آن باید با اعدادِ مختلط و همچنین سری‌های نامتناهی آشنا باشد. تا آنجا که مترجم اطلاع دارد، هیچ کدام از این موضوعات در ریاضیاتِ دبیرستانی آموزش داده نمی‌شوند.

ولی هیچ یک از این موارد مانعی برای مطالعه این کتاب نیست، زیرا نویسنده تلاش کرده تا آنجا که امکان دارد زمینه‌های ریاضی لازم را برای خواننده فراهم آورد.

مورد جالبی که در این کتاب به چشم می‌خورد تقسیم فصول کتاب به بخش‌های فنی و تاریخی است. فصول زوج عمدتاً به موضوعات تاریخی و بیوگرافی، و فصول فرد عمدتاً به موضوعات فنی و ریاضی می‌پردازد. البته در این میان، مخلوطی از اینها نیز به چشم می‌خورد. هستهِ ریاضی کتاب را فصول 13، 15، 17، 19، و 21 تشکیل می‌دهد. گرچه ریاضیاتِ این فصول می‌تواند پیشرفته باشد، ولی همانطور که گفتم، آنها تا آنجا که امکان داشته ساده شده‌‌اند‌ تا برای خوانندگان ترم‌های اول رشته‌های ریاضی/مهندسی، یا حتی آخر دبیرستان قابل درک باشند.

نکته‌ای که مایلم بر آن تاکید کند، اهمیت بخش‌های تاریخی است. بخش عمده‌ای از این کتاب را مطالب تاریخی و شرح‌حالی (بیوگرافیک) تشکیل می‌دهد. تاریخی که در این کتاب از آن صحبت می‌شود بیشتر به تاریخ 300 سالِ اخیرِ اروپا مربوط است، که شاید از دید یک دانشجو یا دانش‌آموزِ جوان ایرانی که رشته او ریاضی/مهندسی است و فقط می‌خواهد نوعی بینش مقدماتی نسبت به فرضیه ریمان کسب کند، ممکن است نامربوط بنظر برسد. ولی از نظر من، این بخش‌ها از اهمیت کلیدی برخوردار هستند زیرا نه فقط زندگی و روحیات افرادی را شرح می‌دهد که به نحوی در فرضیه ریمان دخیل بوده‌اند، بلکه وقایع مهمِ تاریخ اروپا را نیز شرح می‌دهد، وقایع و شخصیت‌هایی که در زمان خودشان بسیار کلیدی و سرنوشت‌ساز بودند. اینها موضوعاتی هستند که در درس‌های تاریخ صحبت زیادی از آنها نمی‌شود، و برای اطلاع از آنها باید به کتاب‌های تخصصی‌تر رجوع کنید. ولی بی‌تردید نمی‌توانید همه آنها را بصورت یکجا داشته باشید، آنهم در قالب یک کتاب ریاضی. اگر می‌خواهید بدانید که چرا پوتین در روسیه محبوب است، یا چرا روسیه درگیر آرمان‌های امروز خود است، همان آرمانهایی که شاید یکی از آنها دلیل حمله او به اوکراین باشد، شما باید به زمان پِطرِ کبیر و کاترین بازگردید، یا اگر می‌خواهید بدانید که چرا آلمان وضعیتی را پیدا کرد که آغاز کننده دو جنگ بزرگ جهانی در قرن بیستم بود، باید به ابتدای قرن نوزدهم، و دوران جنگهای ناپلئونی بازگردید، یا اگر می‌خواهید بدانید چرا جنبش صهیونیسم پا گرفت و نهایتاً به تشکیل اسرائيل منجر شد، باید به پایان قرن نوزدهم و ماجرای دریفوس در فرانسه بازگردید. در این کتاب همه این موضوعات بصورت خلاصه، و البته به شکلی مرتبط با ریاضیات و ریاضیدانان، مرور می‌شوند. اگر شما موضوعات فنی کتاب را دشوار دیدید، تصور می‌کنم فصول زوج کتاب، که شامل بخش‌های تاریخی/بیوگرافی است، به تنهایی می‌تواند جالب و خواندنی باشد.

این کتاب در سال 2002 نوشته شده و اکثر تلاش‌هایی که در راه اثبات فرضیه ریمان انجام گرفته را پوشش می‌دهد. سئوالی که ممکن است مطرح ‌شود این است که آیا بهتر نبود کتاب جدیدتری برای ترجمه انتخاب می‌شد، کتابی که حاوی آخرین پیشرفت‌ها در این زمینه باشد؟ در پاسخ باید بگویم، اگر کتاب جدیدتری را در این سطح پیدا کرده بودم، حتماً آن را برای ترجمه انتخاب می‌کردم، ولی تا آنجا که اطلاع دارم چنین کتابی موجود نبود. از این گذشته، متاسفانه طی 20 سال اخیر، پیشرفتِ عمده‌ای در جهت اثبات این فرضیه صورت نگرفته، مگر چند ادعا از طرف کسانی مثل مایکل عطیه، و دیگران که بعداً نادرستی آنها معلوم شده. بنابراین از لحاظ تاریخی، مطالب این کتاب را می‌توان کامل تلقی کرد. از لحاظ فنی نیز شامل آخرین تلاش‌هایی است که تا ابتدای قرن بیست و یکم در این زمینه صورت گرفته است.

کتاب مورد استفاده چه کسانی است

این کتاب برای افراد کنجکاوی نوشته شده که می‌خواهند با بزرگترین، مهمترین، و سخت‌ترین مسئله ریاضیاتِ امروز آشنا شده، و از اهمیت آن آگاه شوند.

موضوع کتاب حاضر درباره ریاضیات است، و بیان آن تا حدی به ریاضیات پیشرفته نیاز دارد، موضوعاتی که شرح آنها به زبان غیر-ریاضی امکان ندارد. مزیت این کتاب این است که آنها را به ساده‌ترین شکل ممکن بیان کرده. همانطور که نویسنده در مقدمه خودش گفته ”اگر شما پس از اتمام این کتاب هنوز فرضیه ریمان را درک نکرده‌اید، تقریباً می‌توانید مطمئن باشید که هرگز آن را درک نخواهید کرد.“

خیلی از موضوعات علمی دشوار، مثل نظریه نسبیت یا نظریه کوانتوم، را می‌توان برای فهم عموم به شکل غیر-ریاضی بیان کرد (برای نمونه به کتاب سیاه‌چاله‌ها کرم‌چاله‌ها و ماشین‌های زمان رجوع کنید). ولی موضوعاتی هستند که اگر به شکل غیر-ریاضی بیان شوند، معنی خود را از دست می‌دهند (مثل موضوع کتاب حاضر). یک سال پس از انتشار این کتاب، ریاضیدان و مجری برنامه‌های تلویزیونی، مارکوس دو ساتوی (Marcus du Sautoy) یک کتابِ مقدماتی، بنام ”موسیقی اعداد اول“ نوشت، که موضوع آن هم درباره اعداد اول و فرضیه ریمان بود. با اینکه آن کتاب توسط ریاضیدانی نوشته شده بود که حوزه تحقیقاتی او اعداد اول است، و با ریاضیاتِ اندکی هم که در آن بکار رفته، نسبت به کتاب حاضر ساده‌تر بود، ولی تنها چیزی که پس از مطالعه آن دستگیرتان می‌شود این است که فرضیه ریمان بسیار مهم است، ولی چرا ... خیلی معلوم نیست.

درباره نویسنده

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image003.png$ جان داربی‌شِر (John Derbyshire) متولد 1945، دانش‌آموخته ریاضی از دانشگاه لندن است. او نویسنده، روزنامه‌نگار، و برنامه‌نویس کامپیوتر است. وی در انگلستان متولد شد و در 30 سالگی تابعیت آمریکا را نیز گرفت. از لحاظ سیاسی، داربی‌شِر یک محافظه‌‌کارِ ملی‌گرا محسوب می‌شود، ولی نه شبیه کسانی مانند دونالد ترامپ، یا حتی جورج بوش. او گفته بود از بسیاری جهات طرفدار هیلاری کلینتون است. او حتی در اوایل دهه 1970 در فیلم اکشن”راهِ اژدها“ با بازی بروس لی، نقش کوچکی را داشت. به دلیل علاقه‌ای که به فرهنگ چینی دارد، او نهایناً با یک زن چینی تبار ازدواج کرد، که بعداً به شهروندی آمریکا درآمد. همانطور که معلوم است، با نویسنده‌ رنگارنگی روبرو هستیم که زمینه‌های فکری و کاری متنوعی دارد.

داربی‌شِر با اینکه مدرک خودش را در ریاضیات گرفته، ولی یک ریاضیدان حرفه‌ای نیست و خودش هم چنین ادعایی ندارد. چیزی که این کتاب را از کتاب‌های یک ریاضیدان حرفه‌ای (نظیر یان استوارت، که من از او چند کتاب ترجمه‌ کرده‌ام) متمایز می‌کند، قابلیت‌های روزنامه‌نگاری اوست. رویکردی که او در تدوین این کتاب اتخاذ کرده، شبیه یک روزنامه‌نگارِ محقق است. به همین دلیل، او برای موضوع کتابش تحقیقات زیادی کرده، و در واقع این کتاب حاصل مصاحبه‌های زیادی بوده که او با ریاضیدانان معاصر انجام داده.

بیشتر نوشته‌های داربی‌شِر به سیاست و جامعه‌شناسی مربوط‌‌ند و آثار ریاضی او اندک‌ است، ولی یکی دو کتابی هم که درباره ریاضیات نوشته برجسته و خواندنی هستند. کتاب حاضر، در سال 2004 برنده جایزهِ کتابِ انجمن ریاضی آمریکا شده. این نویسنده کتاب دیگری با عنوان ”کمیت مجهول“ دارد، که موضوع آن نیز درباره ریاضیات است. فعلاً درحال ترجمه آن هستم، و انشاالله همین امسال منتشر خواهد شد.

بهار 1401

کامران بزرگزاد

مقدمه مؤلف

در ماه آگوست سال 1859، برنهارت ریمان (Bernhard Riemann) به عضویت افتخاری آکادمی برلین برگزیده شد، برای یک ریاضیدان جوان، این مایه افتخار بزرگی بود (در آن زمان او تنها 32 سال داشت). همانطور که در چنین مراسمی مرسوم بود، ریمان مقاله‌ای را به آکادمی تسلیم کرد که حاوی برخی تحقیقاتی بود که او در آن موقع به آنها مشغول بود. عنوان مقاله این بود: ”در باب تعداد اعداد اول که از یک کمیت مفروض کوچکتر هستند.“ ریمان در این مقاله بر روی موضوع خاصی در حسابِ عادی تحقیق کرده بود. برای درک این موضوع، مثلاً می‌توانید این سئوال را بپرسید که ” تعداد اعدادِ اولی که کمتر از 20 هستند چقدر است؟ جواب 8 است: 2، 3، 5، 7، 11، 13، 17، و 19. برای عددی مثل 1000 این تعداد چقدر است؟ برای یک میلیون چطور؟ برای یک بیلیون چقدر؟ آیا برای بدست آوردن این مقادیر، یک قاعده یا فرمولِ کلی وجود دارد تا مجبور نباشیم اعداد اول کوچکتر از آنها را یکی یکی بشماریم؟

ریمان با استفاده از پیچیده‌ترین ریاضیاتِ زمانِ خودش به جنگ این مسئله رفت، و برای اینکار از ابزارهایی بهره گرفت که حتی امروز هم فقط در درس‌های پیشرفته دانشگاهی تدریس می‌شوند، و برای هدف خودش یک شیء ریاضی را ابداع کرد که قدرت و ظرافت بسیاری داشت. او در صفحات ابتدایی مقاله خودش درباره آن شیء، که تابع زتا نام دارد، حدسی را مطرح کرد، و سپس اظهار داشت:

البته همه می‌خواهند برای اینمورد یک اثبات قوی داشته باشند، ولی پس از چند تلاش بیهوده، من از جستجو برای یافتن چنین اثباتی دست کشیدم، زیرا چنین چیزی برای هدف فعلی من ضروری نیست.

این حدسِ فرعی و غیر-ضروری، برای دهه‌ها مورد توجه قرار نگرفت. سپس، بنا به دلایلی که در این کتاب شرح خواهم داد، به تدریج مورد توجه ریاضیدانان قرار گرفت، تا آنجا که به یک دغدغه طاقت‌فرسا بدل شد.

این حدس، که بعداً فرضیه ریمان (Riemann Hypothesis) نامیده شد، در طول قرن بیستم، و تا به امروز بعنوان یک دغدغه باقی مانده، و در برابر تمام تلاش‌هایی که برای اثبات یا ابطال آن بعمل آمده مقاومت کرده. امروزه این دغدغه حقیقتاً قویتر نیز شده، زیرا حالا خیلی از مسائل قدیمی، که قبلاً لاینحل بودند، بنحوی حل شدند، به جز این مسئله. از میان این مسائل می‌توان به قضیه چهار-رنگ (که در سال 1852 مطرح، و در سال 1972 اثبات شد)، آخرین قضیه فرما (که در سال 1637 مطرح، و در سال 1994 اثبات شد)، و بسیاری از مسائل دیگر اشاره کرد که خارج از دنیای ریاضیاتِ حرفه‌ای معروفیت زیادی ندارند. حالا فرضیه ریمان به دست نیافتنی‌ترین موضوع ریاضیات نوین بدل شده.

تمامی قرن بیستم با شیفتگی ریاضیدانان نسبت به فرضیه ریمان همراه بود. در دومین کنگره بین‌المللی ریاضیدانان که در سال 1900 در پاریس برگذار ‌شد، داوید هیلبرت (David Hilbert)، که یکی از برجسته‌ترین ریاضیدانان عصر خودش بود، خطاب به حضار اینطور گفت:

اخیراً کسانی مانند آدامار (Hadamard)، دو لا والی پوسان (de la Vallée Poussin)، فون مندگولدت (Von Mangoldt)، و دیگران، پیشرفت‌های اساسی در نظریه توزیع اعداد اول حاصل کرده‌اند. ولی برای حل کامل مسائلی که مقاله ریمان، تحت عنوان ”در باب تعداد اعداد اول کوچکتر از یک کمیت مفروض“، پیش روی ما نهاده، هنوز هم باید صحت اظهارات مهم ریمان اثبات شود، مثلاً ...

و بدنبال آن فرضیه ریمان را مثال می‌زند. صد سال بعد در ماه ژانویه 2000، مدیر موسسه تحقیقاتِ پیشرفته پرینستون و استاد بازنشسته ریاضیات دانشگاه هاروارد، فیلیپ گریفیتس (Phillip Griffiths)، در مقاله‌ای که در مجله American Mathematical Monthly ، تحت عنوان ”چالش‌های تحقیقاتی قرن بیست و یکم“ چاپ کرد، می‌گوید:

علی‌رغم دست‌آوردهای عظیمی که در قرن بیستم به عمل آمده، چندین مسئله هستند که هنوز باید حل شوند. احتمالاً بسیاری از ما موافق هستیم که سه مسئله زیر، مهمترین چالش‌های ما را تشکیل می‌دهند:

فرضیه ریمان اولین چالشی است که در طول150 سال گذشته ریاضیدانان را آزار می‌دهد ...

تحول جالبی که در طول سالهای آخر قرن بیستم در آمریکا پدید آمد، ظهور دو موسسه خصوصی برای تحقیقات ریاضی بود که توسط افراد ثروتمند و دوستار ریاضیات بنیان نهاده شدند. یکی موسسه ریاضی کلِی (Clay Mathematics Institute) بود که در سال 1998 توسط لندون کلی تاسیس شد، و دیگری موسسه ریاضی آمریکا، که در سال 1994 توسط جان فرای (John Fry) تاسیس گردید. هر دو این موسسات فرضیه ریمان را هدف قرار دادند. موسسه کلِی یک جایزه یک میلیون دلاری برای اثبات یا ابطال آن درنظر گرفت؛ موسسه ریاضی آمریکا هم با ارائه سه کنفرانسِ تمام عیار در سال‌های 1996، 1998، و 2002، که در آن ریاضیدانانی از سراسر جهان حضور داشتند، به جنگ این مسئله رفت. اینکه آیا این مشوق‌ها و رویکردهای جدید سرانجام موجب درهم شکستن فرضیه ریمان می‌شوند یا نه، این چیزیست که بعداً مشخص می‌شود.

بر خلاف قضیه چهار-رنگ، یا آخرین قضیه فِرما، بیان فرضیه ریمان به زبان غیر-ریاضی، کمی دشوارتر است. این مسئله در قلب برخی از غامضترین نظریه‌های ریاضی قرار دارد، و صورت مسئله آن این است:

فرضیه ریمان می‌گوید که جزء حقیقی کلیه صفر‌های غیر-ساده تابع زتا، $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image005.png$ هستند.

از نظر یک خواننده عادی، حتی کسی که تحصیلات عالی دارد، و هیچ درس ریاضیات پیشرفته را نگذرانده باشد، احتمالاً چنین مسئله‌ای کاملاً غیرقابل درک است. عبارت فوق شبیه عبارتی است که به زبان اسلاوِ باستان [1] نوشته شده، و هیچ کس بجز آنهایی که اهل کلیسای شرق باشند معنی آن را نمی‌فهمد. در این کتاب تلاش من بر این است که علاوه بر شرحِ تاریخچه این فرضیه، و برخی از اشخاصی که با آن درگیر بوده‌اند، با ارائه اندکی ریاضیات، طوری آن را بیان کنم که درخور درک یک خواننده عادی باشد.

*****

طرح کتاب بسیار ساده است. فصولی که شماره آنها فرد هستند حاوی توضیحات ریاضی هستند، که امیدوارم خواننده را به فهم فرضیه ریمان و اهمیت آن هدایت کند. فصولی که شماره آنها اعداد زوج هستند به شرح موارد تاریخی و شرح حال افراد درگیر در این مسئله می‌پردازد.

هدف اولیه من این بوده که این دو مسیر مستقل از یکدیگر باشند، تا خوانندگانی که از معادلات و فرمول‌ها خوششان نمی‌آید فقط بتوانند فصول زوج را بخوانند، و خوانندگانی که تاریخ و حکایات برای آنها اهمیت زیادی ندارد بتوانند روی فصول فرد تمرکز کنند. البته به علت پیچیدگی موضوع، پیروی از این رویکرد دشوار بود و در بعضی موارد من نتوانستم بطور دقیق آن را دنبال کنم. بنابراین باید بگویم میزان ریاضیات گنجانده شده در فصول فرد نسبت به فصول زوج بیشتر است، و شما مجاز هستید که هر کدام از این فصول را که تمایل دارید مطالعه کنید. البته امیدوارم شما کل کتاب را بخوانید.

مخاطبین این کتاب خوانندگانِ باهوش و کنجکاوی هستند، که ضرورتاً ریاضیات پیشرفته نمی‌دانند. البته عبارت فوق این سئوال را پیش می‌آورد که منظور از ”آنهایی که ریاضیات پیشرفته نمی‌دانند“ چه کسانی است؟ برای درک کامل این کتاب به چه مقدار ریاضیات نیاز است؟ البته همه مقداری ریاضیات می‌دانند. احتمالاً بیشتر افراد تحصیل کرده مختصراً می‌دانند که حسابان چیست. فکر می‌کنم کتاب را با این فرض تنظیم کرده‌ام که خواننده این کتاب ریاضیات دبیرستانی را تمام کرده و شاید چند درس دانشگاهی را نیز گذرانده باشد. در واقع هدف اصلی من این بود که فرضیه ریمان را بدون اینکه هیچ استفاده‌ای از حسابان بکنم شرح دهم. البته ثابت شده که چنین چیزی کمی خوشبینانه است، و مقدار اندکی از حسابانِ مقدماتی در سه فصل خواهد آمد.

غیر از اینها، آنچه مورد نیاز است فقط حساب و جبر ساده است: چیزهایی مثل ضرب عبارات جبری ساده (a+b)×(c+d)، یا ساده کردن معادلاتی مثل S=1+xS، که بصورت S=1 ⁄(1–x) ساده شوند. شما همچنین باید با ساده‌ کردن عبارات جبری آشنا باشید. کمترین ادعایی که من دارم، این است که فکر نمی‌کنم فرضیه ریمان بتواند ساده‌تر از آنچه من در این کتاب شرح داده‌ام، و کمترین استفاده از ریاضیات، شرح داده شود. بنابراین اگر شما پس از اتمام این کتاب هنوز فرضیه ریمان را درک نکرده‌اید، تقریباً می‌توانید مطمئن باشید که هرگز آن را درک نخواهید کرد.

*****

موضوعاتی که در این کتاب آمده برای حدود صد پنجاه سال بطور مستمر و متمرکز توسط بهترین ریاضیدانان جهان مورد پژوهش قرار گرفته‌اند. روش‌هایی که من برای شرح این موضوعات برگذیده‌ام، و آنچه در تدوین این کتاب در دسترس من بوده، ایجاب می‌کرده که بسیاری از حوزه‌های مرتبط با فرضیه ریمان را کنار بگذارم. در این کتاب شما از مباحثی مانند فرضیه چگالی (Density Hypothesis)، تقریب معادله تابعی، و بسیاری از موضوعات جالب دیگر که اخیراً در رابطه با تابع زتا حاصل شده، اثری نمی‌بینید. همچنین به فرضیه ریمانِ تعمیم‌یافته، فرضیه ریمانِ تغییریافته، فرضیه ریمان توسعه ‌یافته، فرضیه ریمانِ تغییریافته بزرگ، یا قضیه شِبه-ریمانی هیچ اشاره‌ای نمی‌شود.

بدتر از این، عدم اشاره به نام کسانی است که در دهه‌های اخیر مجدانه در این زمینه فعالیت داشته‌اند، کسانی مثل: Enrico Bombieri، Amit Ghosh، Steve Gonek، Henryk Iwaniec، Nina Snaith، و بسیاری از ریاضیدانان دیگر. از این بابت، من صمیمانه از آنها پوزش می‌طلبم. حجم این کتاب می‌توانست نسبت به آنچه که حالا هست، 3 برابر، یا حتی 30 برابر، بیشتر باشد.

معمولاً یک کتاب به کسی تقدیم می‌شود که زنده باشد، و مایه خشنودی او شود. من نیز این کتاب را به همسرم تقدیم می‌کنم، کسی که به خوبی می‌داند این تقدیم چقدر از روی عشق است. ولی این را نیز نباید در مقدمه نادیده بگیرم که این کتاب به برنهارت ریمان تعلق دارد، کسی که در عمر کوتاهش با بدبختی‌های فراوانی دست و پنجه نرم کرد، و نهایتاً برای همنوعانش میراث بسیار عظیمی بجا گذاشت، از جمله مسئله‌ای که اکنون بیش از صد و پنجاه سال است ریاضیدانان با آن کلنجار می‌روند، چیزی که خودش از آن بعنوان ”تلاش‌های بیهوده“ یاد کرده بود.

جان داربی‌شِر، نیویورک

ژوئن 2002

22/08/95

فصل 1

ترفند ورق‌های بازی

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image006.png$

1.

25/10/1400

مانند بسیاری از ترفند‌ها، در اینجا نیز ما کار خودمان را با یک دست ورق بازی شروع می‌کنیم.

یک دسته ورق بازی 52تایی را در نظر بگیرید که روی یک میز قرار گرفته، و چهار سمت کارت‌ها بطور مرتب روی هم قرار دارند. حالا بدون اینکه کارت‌های دیگر تکان بخورند، کارت بالایی را با یک انگشت به جلو بلغزانید. چقدر می‌توانید این کارت را بدون اینکه کج شود و نهایتاً بی‌افتاد، به جلو بلغزانید؟ یا به عبارت دیگر، چقدر می‌توانید آن را روی بقیه کارت‌ها معلق نگاه دارید؟

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image007.png$

شکل 1-1

پاسخ این است که، همانطور که در شکل 1-1 نشان داده شده، شما می‌توانید به اندازه نصف طول یک کارت آن را به جلو بلغزانید. اگر آن را بیشتر از نصف طول یک کارت به جلو بلغزانید، پایین می‌افتاد. جواب دقیقتر این است که تا نقطه‌ای می‌توانید آن را به جلو بلغزانید که مرکز ثقل کارت باشد، که می‌شود نصف طول آن.

کارت بالایی که تا نیمه طول جلو آمده را رها کرده و حالا کارت دوم را به جلو بلغزانید. در این وضعیت، شما چقدر می‌توانید کارت دوم را بدون اینکه سقوط کند به جلو بلغزانید؟

ترفند این است که دو ورق بالایی را به عنوان یک واحدِ منفرد در نظر بگیرید. مرکز ثقل این واحد در کجا قرار دارد؟ خوب، جواب مانند قبل نیمه طول این واحد است، که مجموعاً طول آن می‌شود (1+½=³/₂)، که نصف آن می‌شود ³/₄. بنابراین جواب این است به اندازه سه چهارم طول یک کارت از نقطه آویز (به شکل 2-1 نگاه کنید). بنابراین طولِ ترکیبی این واحدِ معلق به اندازه سه چهارم طول یک کارت است. توجه داشته باشید که کارت بالایی هنوز هم به اندازه نصف طول یک کارت معلق است. شما دو کارت بالایی را بعنوان یک واحدِ منفرد حرکت داده‌اید.

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image008.png$

شکل 2-1

حالا اگر شروع کنید سومین کارت را حرکت دهید، در اینصورت خواهید دید که می‌توانید آن را به اندازه یک ششم طول یک کارت حرکت دهید. ترفند کار در اینجا نیز این است که سه کارت بالایی را بعنوان یک واحدِ منفرد در نظر بگیرید. مرکز ثقل این واحد عبارت است از یک-ششم طول یک کارت از لبه‌ معلق شده کارت سوم (شکل 3-1 را ببینید).

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image009.png$

شکل 3-1

در جلو این نقطه، یک-ششم کارت سوم، یک-ششم بعلاوه یک چهارم کارت دوم، و یک-ششم بعلاوه یک چهارم + یک دوم کارت بالایی است، که طول کل آن را یک و یک دوم کارت می‌کند.

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image010.png$

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image011.png$

شکل 4-1

یعنی نصف سه کارت (نصفه دیگر پشت نقطه تعلیق قرار دارد)، و این حالتی است که می‌توانید پس از حرکت دادن کارت سوم به آن برسید (شکل 4-1 را ببینید).

حالا طول کلی واحدِ معلق می‌شود: یک دوم از کارت بالایی، بعلاوه یک چهارم از کارت دوم، بعلاوه یک ششم از کارت سوم. یعنی یازده دوازدهم، ¹¹/₁₂. شگفت انگیز است!

آیا می‌توانیم کارت دیگری را نیز حرکت دهیم و باز هم تعادل را حفظ کنیم؟ البته! اگر کارت بعدی، یعنی چهارمین کارت از بالا را با دقت به اندازه یک هشتمِ طول یک کارت حرکت دهید، نقطه تعادل بعدی را خواهید داشت. اینجا من قصد ندارم محاسبات را تکرار کنم؛ شما می‌توانید به من اعتماد کنید، یا همانطور که برای سه مرحله قبل انجام دادم، خودتان آن را حساب کنید. طول کارت‌های معلق برای چهار کارت عبارت است از: یک دوم بعلاوه یک چهارم بعلاوه یک ششم بعلاوه یک هشتم، که می‌شود یک و یک‌بیست و چهارم (شکل 5-1 را ببینید).

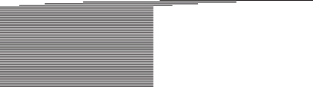
$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image012.png$

شکل 5-1

اگر به همین ترتیب این را برای 52 کارت تکرار کنید، طول کلی کارت‌های معلق عبارت خواهد بود از:

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image013.png$

این برای شما سایه‌بانی به طول 2.25940659073334 ایجاد می‌کند. بنابراین طول کارت‌های معلق چیزی در حدود دو و یک-چهارم طول یک کارت خواهد بود (شکل 6-1 را ببینید).

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image014.png$

شکل 6-1. سایبانی از 52 کارت معلق به طول 2.25940659073334.

زمانی که من این را یادگرفتم دانشجو بودم. تعطیلات تابستانی بود و من برای ‌تِرم بعدی آماده می‌شدم، و سعی داشتم دروس مربوطه را پیش‌تر بخوانم. برای اینکه مخارج دانشگاه را بپردازم، تابستان‌ها بعنوان یک کارگر ساختمانی کار می‌کردم. روز بعدِ اینکه این مسئله را یادگرفتم، یک کار تمیزکاری به من محول شد. در آنجا صدها آکوستیک سقفیِ مربع شکل روی‌هم انباشته شده بود. من یک ساعتی را با آنها کلنجار زدم و تلاش کردم 52 عدد از آنها را روی هم معلق کنم. پس از آن سر و کله سرکارگر پیدا شد و من را دید که کاملاً محو فکر کردن درباره این برج معلق شده‌ام. فکر ‌کنم آن موقع پیش خودش گفته بود که دیگر هرگز یک دانشجو را استخدام نکند!

2.

یکی از کارهایی که ریاضیدانان به آن علاقه دارند، و آن را مفید می‌دانند، عمل برون‌یابی (extrapolation) است. برون‌یابی یعنی با در نظر داشتن معلومات یک مسئله، سعی کنیم آن را گسترش دهیم تا موارد بیشتری را پوشش دهد.

در بالا من فرض را بر این گذاشتم که ما برای کار خودمان 52 کارت داریم. معلوم شد که ما می‌توانیم آویزی درست کنیم که طول آن کمی بیش از $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image015.png$ طول یک کارت باشد.

ولی چرا خودمان را به 52 کارت محدود کنیم؟ اگر تعداد آنها را بیشتر کنیم، مثلاً صد کارت، یا هزار کارت، یا یک میلیون کارت، در آن صورت مسئله به چه صورت درمی‌آید؟ اگر ما تعداد نامحدودی کارت داشته باشیم، آن وقت چه می‌شود؟ حداکثر طولِ ممکن که با روی هم چیدن این کارت‌ها می‌توانیم بدست آوریم چقدر است؟

ابتدا بیایید به صورت اولیه مسئله، یعنی 52 کارت باز گردیم. با 52 کارت، طول واحد معلق ما این بود:

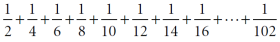
$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image016.png$

بدلیل اینکه کلیه مخرج‌ها زوج هستند، ما می‌توانیم از ½ فاکتور بگیریم و مجموع بالا را بصورت زیر بنویسیم:

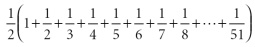
$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image017.png$

اگر صد کارت داشته باشیم، در این صورت طول واحد معلق عبارت است از:

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image018.png$

و اگر یک تریلیون کارت داشته باشیم:

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image019.png$

بدست آوردن حاصل اینها محاسبات سنگینی را می‌طلبد، ولی ریاضیدانان برای اینجور چیزها راه‌های میانبری دارند، و من می‌توانم با اطمینان به شما بگویم که برای صد کارت طول واحد معلق کمی کمتر از 2.58868875882، و برای یک تریلیون کارت کمی بیشتر از 14.10411839041479 است.

از دو جهت این اعداد شگفت‌انگیز هستند. اول اینکه شما می‌توانید یک طول معلق به اندازه طول 14 کارت داشته باشید، ولی برای دستیابی به آن نیاز به یک تریلیون کارت دارید. طول 14 کارت معمولی تقریباً صد و سی سانتی متر است. شگفتی دوم این است که نسبت به مسئله اولیه، طول‌های بدست آمده خیلی بزرگتر نیستند. اگر از 52 کارت به 100 کارت بروید، اضافه طولی در حدود یک-سوم طول یک کارت خواهید داشت. اگر از یک تریلیون کارت استفاده کنید، طولِ واحد معلق شما نسبت به قبل، تنها به اندازه یازده و یک-دوم (11½) طول یک کارت اضافه می‌شود (اگر یک تریلیون کارت معمولی روی هم چیده شوند، ارتفاع آنها تقریباً به اندازه فاصله کره زمین تا ماه است!)

اگر تعداد نامحدودی کارت روی‌ هم چیده شوند وضعیت به چه صورت درمی‌آید؟ حداکثر طولی که یک واحد معلق می‌تواند داشته باشد چقدر است؟ پاسخ جالب توجه این است که هیچ حداکثری برای این طول وجود ندارد. اگر به اندازه کافی کارت در اختیار داشته باشید، شما می‌توانید به هر طولی که دلتان می‌خواهد برسید. مثلاً اگر بخواهید طول واحد معلق شما به اندازه طول 100 کارت باشد، باید در حدود 405,709,150,012,598 تریلیون، تریلیون، تریلیون، تریلیون، تریلیون، تریلیون کارت را روی هم بچینید. ارتفاع این دسته از کارت‌ها، از اندازه کل جهانِ مریی نیز خیلی خیلی بیشتر است. ولی اگر از کارت‌هایی استفاده کنید که تعداد آنها بطور غیرقابل تصوری زیاد باشد، شما می‌توانید به هر طولی که می‌خواهید برسید. آیا می‌توانیم طولی به اندازه یک میلیون کارت را داشته باشیم؟ البته که می‌توانیم، ولی تعداد کارت‌های لازم برای اینکار به قدری زیاد است که نوشتن آنها در یک کتاب معمولی هم جا نمی‌گیرد، در واقع این یک عدد 868,589 رقمی است.

3.

چیزی که در اینجا باید به آن توجه کرد عبارت داخل پرانتز است، یعنی

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image020.png$

این همان چیزی است که ریاضیدانان به آن یک سری (series) می‌گویند، یعنی مجموع جملاتی که بطور نامعینی ادامه دارند، و جملات بعدی آن با یک تصاعدِ منطقی به دنبال هم می‌آیند. در اینجا جملات
$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image021.png$ ، وارون اعداد شمارشی 1, 2, 3, 4, 5, 6, 7, … هستند.

سری $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image022.png$ بقدری اهمیت دارد که ریاضیدانان نام سری هارمونیک (Harmonic series) را به آن داده‌اند.

آنچه در بالا بیان کردم به این صورت خلاصه می‌شود که: اگر به اندازه کافی جملات سری هارمونیک را با هم جمع کنید، شما می‌توانید به هر عددی بزرگی که مورد نظرتان برسید، زیرا این مجموع حدی ندارد.

چنین چیزی را می‌توانیم با یک عبارت زمخت، ولی گویا، نیز بیان کنیم: ”مجموع سری هارمونیک بی‌نهایت است“

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image023.png$

ریاضیدانانی که خوب آموزش دیده‌اند، می‌‌دانند که باید از چنین عباراتی پرهیز کنند؛ ولی تا زمانی که شما از دام‌هایی که چنین عباراتی می‌توانند برای شما پهن کنند آگاه باشید، فکر می‌کنم کاربرد آنها کاملاً بجا باشد. لئونارد اویلر (Leonhard Euler)، که یکی از ده ریاضیدان بزرگ تاریخ بود، همیشه از چنین فرمول‌هایی استفاده می‌کرد و نتایج پرباری را نیز بدست می‌آورد. ولی امروزه اصطلاحِ درستی که برای عبارت فوق بکار می‌برند این است: سری هارمونیک واگرا (divergent) است.

خوب، من واگرا بودن سری هارمونیک را توضیح دادم، ولی آیا می‌توانم آن را اثبات کنم؟ همه می‌دانند که در ریاضیات هر چه قدر هم که ظاهر چیزی درست باشد، نمی‌توان به درستی آن اعتماد کرد، بلکه صحت آن باید با یک منطقِ محکم اثبات شود. در اینجا نتیجه‌ای که ما گرفته‌ایم این است: سری هارمونیک واگرا است. ولی چگونه می‌توان آن را اثبات کرد؟

در واقع اثبات این قضیه ساده است، و به چیزی غیر از حساب معمولی نیاز ندارد. این اثبات در اواخر قرون وسطی (در حدود 1382-1323 میلادی) توسط دانشمند فرانسوی نیکول اورسم (Nicole Oresme) بیان شد. اورسم یاد آور شد که $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image024.png$ از $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image005.png$ بزرگتر است؛ همینطور $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image025.png$ نیز از $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image005.png$ بزرگتر است؛ و این درمورد $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image026.png$ و غیره نیز صادق است. به عبارت دیگر، کاری که در اینجا باید انجام دهید این است که سری هارمونیک را به گروه‌های 2 جمله‌ای، و بعد 4 جمله‌ای، و بعد 8 جمله‌ای و بعد 16 جمله‌ای، و غیره گروه‌بندی کنید. بنابراین، شما تعداد بی‌نهایتی از گروه‌ها را خواهید داشت که همه از $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image005.png$ بزرگتراند. پس مجموع آنها نیز بی‌نهایت خواهد بود. از اینکه در هر مرحله تعداد اعضای گروه‌ بزرگتر و بزرگتر می‌شوند سردرگم نشوید. در ”بی‌نهایت“ اطاق‌های بی‌شماری برای گروه‌بندی وجود دارد، و هر تعداد گروه هم که داشته باشید، جا برای گروه بعدی شما هست. همیشه یک بلوک طولانی هست که حاصل جمع آن از $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image005.png$ بزرگتر است، بنابراین حاصل جمع این بلوک‌ها نیز بدون محدودیت زیاد می‌شود.

اثبات اورسم برای واگرا بودن سری هارمونیک برای قرن‌ها از نظرها پنهان ماند. تا آنکه در سال 1647 پیترو منگولی (Pietro Mengoli) با استفاده از روش متفاوتی آن را دوباره اثبات کرد؛ چهل سال بعد، یوهان برنولی (Johann Bernoulli) باز هم آن را با روش دیگری اثبات کرد؛ و مدت کوتاهی پس آن، ژاکوب برادر بزرگتر یوهان، آن را به روش دیگری اثبات نمود. بنظر می‌رسد که نه منگولی و نه برادران برنولی از اثبات قدیمی اورسم آگاهی داشتند. روش اورسم یکی از معدود شاهکارهای اثباتِ ریاضی در قرون وسطی است که تا به حال بجا مانده. این اثبات ساده‌ترین و سرراست و زیباترین اثبات این قضیه است، و همان اثباتی است که امروزه در کتاب‌های درسی به آن اشاره می‌شود.

4.

نکته‌ای که درباره سری‌ها وجود دارت این نیست که برخی از آنها واگرا هستند، بلکه شگفت‌انگیز این است که بعضی از آنها واگرا نیستند. اگر شما تعداد بی‌نهایتی از اعداد را با هم جمع کنید انتظار دارید حاصل جمع آنها نیز بی‌نهایت باشد، اینطور نیست؟ ولی می‌توان نشان داد که همیشه اینطور نیست.

یک خط‌کش معمولی را درنظر بگیرید که بصورت، یک‌دوم، یک‌چهارم، یک‌هشتم، یک‌شانزدهم، و غیره مندرج شده (هر چه دقت بالاتر باشد بهتر است). یک مداد نوک‌تیز را روی نقطه صفر بگذارید، مداد را یک واحد به سمت راست حرکت دهید. حالا مداد به یک سانتی اشاره می‌کند، و شما کلاً آن را یک سانت حرکت داده‌اید (به شکل 7-1 نگاه کنید).

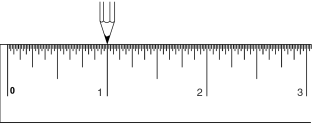
$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image027.png$

شکل 7-1

حالا مداد را نیم‌سانت بیشتر به سمت راست حرکت دهید (به شکل 8-1 نگاه کنید).

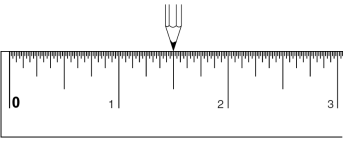
$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image028.png$

شکل 8-1

حالا مداد را به اندازه یک چهارم سانت به راست حرکت دهید ... و بعد یک هشتم سانت ... بعد یک‌شانزدهم... یک سی‌ و دوم .... و یک شصت و چهارم. در اینصورت نوک مداد شما در مکانی قرار دارد که در شکل 9-1 نشان داده شده است:

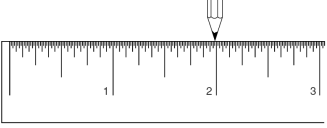
$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image029.png$

شکل 9-1

... و میزانِ کُل فاصله‌ای که شما به سمت راست حرکت کردید برابر است با:

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image030.png$

و همانطور که می‌بینید این فاصله با $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image031.png$ برابر است. مشخص است که اگر این روند را ادامه دهید و هر بار فاصله را نصف کنید، شما به نقطه 2 سانتی نزدیک و نزدیکتر می‌شوید. شما بطور کامل به آن نخواهید رسید، ولی هیچ حدی نیز برای نزدیک شدن به آن وجود ندارد. شما می‌توانید به یک میلیونیم دو سانت؛ یک تریلیونیم دو سانت؛ یک تریلیون تریلیون تریلیون تریلیون تریلیون تریلیونیم دو سانت برسید. ما می‌توانیم این حقیقت را بصورت عبارت زیر بیان کنیم:

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image032.png$

عبارت 1-1

نکته مهم این است که تعداد جملات سری بالا باید بی‌نهایت باشد تا مجموع آنها به 2 برسد.

نکته‌ای که در اینجا می‌خواهم بر آن تاکید کنم، تفاوت این سری جدید با سری هارمونیک است. در سری هارمونیک با جمع کردن تعداد بی‌نهایتی از جملات، حاصلِ جمع آنها نیز بی‌نهایت می‌شود. ولی در سری فوق، حاصل جمعِ بی‌نهایت جمله، 2 می‌شود. سری هارمونیک واگرا، و سری بالا هم‌گرا (convergent) است.

سری هارمونیک شگفتی‌های خاصِ خودش را دارد، و هسته مرکزی فرضیه ریمان را تشکیل می‌دهد، که موضوع اصلی این کتاب است. ولی در کل، ریاضیدانان بیشتر به سری‌های هم‌گرا علاقه دارند تا سری‌های واگرا.

5.

حالا فرض کنید که بجای اینکه همیشه در جهت راست حرکت کنیم، در هر مرحله جهت حرکت خودمان را تغییر دهیم؛ یعنی یک سانت به راست، سپس نیم سانت به چپ، سپس یک چهارم به راست، بعد یک هشتم به چپ و ... . بعد از هفت حرکت، مکانی که نوک مداد من قرار خواهد گرفت در شکل 10ـ1 نشان داده شده است:

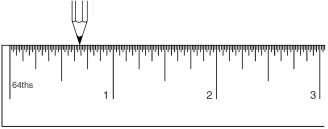
$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image033.png$

شکل 10-1

به دلیل اینکه حرکت به چپ از لحاظ ریاضی مانند یک حرکت منفی به راست است، بنابراین مجموع حرکات ما عبارت خواهد بود از:

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image034.png$

که می‌شود $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image035.png$ . من در فصل‌های بعدی ثابت خواهم کرد که در واقع اگر تعداد بی‌‌نهایتی از این جملات را با هم جمع کنید، عبارت زیر را خواهید داشت:

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image036.png$

عبارت 2-1

6.

در این مرحله ما فرض می‌کنیم که بجای بکار بردن خط‌کشی که بصورت یک‌دوم، یک‌چهارم، یک‌هشتم، یک‌شانزدهم، و ... درجه بندی شده، از خط‌کشی استفاده کنیم که بصورت یک‌سوم، یک‌نهم، یک‌بیست‌وهفتم، یک هشتادویکم، و ... درجه بندی شده باشد. به عبارت دیگر، بجای اینکه در هر مرحله درجه‌ها نصف شوند، بر 3 تقسیم شوند. و فرض کنید همان کاری را که قبلاً کردم، حالا نیز تکرار کنم، و هر بار نوک مداد خودم را روی یکی از درجاتِ یک، یک‌سوم، یک‌نهم، یک‌بیست‌وهفتم و .... به سمت راست حرکت دهم (به شکل 11-1 نگاه کنید).

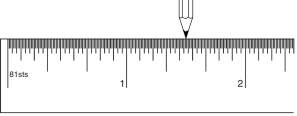
$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image037.png$

شکل 11-1

اگر شما چنین روندی را تا ابد تکرار کنیم، فکر نمی‌کنم مشکل باشد که نهایتاً به فاصله $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image038.png$ از ابتدای حرکت برسید. یعنی

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image039.png$

عبارت 3-1

و البته مانند قبل، من می‌توانم حرکت خودم را بصورت متناوب به راست و چپ انجام دهم: یک سانت به راست، یک‌سوم به چپ، یک‌نهم به راست، یک بیست‌وهفتم به چپ، و ... (به شکل 12-1 نگاه کنید).

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image040.png$

شکل 12-1

نتیجه عبارت زیر خیلی واضح نیست، ولی می‌توان آن را ثابت کرد:

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image041.png$

عبارت 4-1

بنابراین ما چهار سری هم‌گرا داریم، یکی عبارت (1-1)، که به 2 نزدیک و نزدیکتر می‌شود، دومی عبارت (2-1)، که به $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image042.png$ نزدیک و نزدیکتر می‌شود، سومی عبارت (3-1)، که به $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image038.png$ نزدیک و نزدیکتر می‌شود، و چهارمی عبارت (4-1)، که به $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image043.png$ نزدیک و نزدیکتر می‌شود. پیش از معرفی این سری‌های هم‌گرا، من سری دیگری را به شما معرفی کردم که واگرا بود، یعنی سری هارمونیک.

7.

هنگامی که شما یک مطلب ریاضی را می‌خوانید، مهم است بدانید این مطلب به کدامیک از حوزه‌های گسترده ریاضیات تعلق دارد. آن حوزه‌ای که سری‌های بی‌نهایت به آن تعلق دارند، آنالیز (analysis) نام دارد. در واقع از آنالیز برای مطالعه بی‌نهایت‌ها (infinite)، یعنی کمیت‌های بسیار بزرگ، یا بسیار کوچک (infinitesimal) استفاده می‌شد. هنگامی که در سال 1748 لئونارد اویلر (Leonhard Euler)، که من بعداً مطالب بیشتری را در مورد او بیان خواهم کرد، اولین کتاب درسی درباره این موضوع را منتشر کرد، عنوان ”مقدمه‌ای بر آنالیز بی‌نهایت“ را برای آن انتخاب کرد.

در اوایل قرن هجدهم، مفهوم بی‌نهایتِ بزرگ و بی‌نهایتِ کوچک (اینفینی‌تِسی‌مال) مشکلات فراوانی را در ریاضیات ایجاد کرده بود، ولی سرانجام طی یک اصلاحِ گسترده، هر دو مشکل بکلی برطرف شدند. آنالیز نوین چنین مفاهیمی (بی‌نهایت) را مجاز نمی‌شمارد. ولی آنها هنوز هم جزئی از اصطلاحات ریاضیات هستند، و در این کتاب من آزادانه از لغت ”بی‌نهایت“ استفاده خواهم کرد. ولی این استفاده فقط یک میانبر برای یک سری از مفاهیم محکم‌تر است. بطور کلی، امروزه هر گزاره ریاضی که در آن لغت ”بی‌نهایت“ بکار رفته را می‌توان مجدداً طوری فرمول‌بندی کرد که از این لغت استفاده نشود.

مثلاً، وقتی می‌گویم مجموع جملات سری هارمونیک بی‌نهایت می‌شود، منظورم واقعاً این است که هر عددی مانند S را که در نظر بگیریم، هر چقدر هم که بزرگ باشد، نهایتاً مجموع سری هارمونیک از آن بزرگتر خواهد شد. متوجه شدید؟ در اینجا هیچ استفاده‌ای از ”بی‌نهایت“ نشده. در اواخر قرن نوزدهم، کُل حوزه آنالیز ریاضی مجدداً با زبانی بازتعریف شد که در آن از لغت بی‌نهایت استفاده نشده باشد. در ریاضیات نوین، هر گزاره‌ای که نتوان آن را به این صورت نوشت مجاز نیست. گاهی اوقات کسانی که اهل ریاضیات نیستند از من سئوالهایی را می‌پرسند که مثلاً : ” تو که ریاضی می‌دونی به من بگو بی‌نهایت تقسیم بر بی‌نهایت چی میشه؟“ چیزی که من در جواب می‌توانم بگویم این است که ” آنچه شما می‌گویید معنی نمی‌دهد.“ این سئوال، یک جمله ریاضی نیست. در این سئوال طوری از ”بی‌‌نهایت“ حرف زده می‌شود که گویی یک عدد است. بی‌نهایت یک عدد نیست. همینطور اگر خیلی بامزه باشید ممکن است بپرسید ”حاصلِ تقسیمِ حقیقت بر زیبایی چقدر می‌شود؟“ من اصلاً پاسخ آن را نمی‌دانم. تنها چیزی که من می‌دانم این است که چطور اعداد را بر یکدیگر تقسیم کنم. چیزهایی مثل ’بی‌نهایت‘، ’حقیقت‘، ’زیبایی‘، ... عدد نیستند.

پس برخلاف آنچه اویلر گفته بود، تعریف جدید آنالیز چیست؟ در این مرحله، فکر می‌کنم ”مطالعه حدود“ پاسخ مناسبی باشد. مفهوم حَد (limit) در قلب آنالیز قرار دارد. برای مثال، تمامی حسابان (calculus) که بخش عمده آنالیز را تشکیل می‌دهد، بر پایه مفهوم حد قرار دارد.

دنباله $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image044.png$ را در نظر بگیرید. هر جمله جدید توسط یک قاعده ساده از روی جمله قبلی ساخته می‌شود: صورت و مخرج جمله قبلی را با هم جمع کنید تا مخرج جمله جدید بدست آید، صورت جمله قبلی را با دو برابر مخرج آن جمع کنید تا صورت جمله جدید بدست آید. این دنباله به $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image045.png$ همگرا می‌شود. برای مثال، اگر کسر $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image046.png$ را به توان 2 برسانید، حاصل آن $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image047.png$ می‌شود، که اگر آن را حساب کنید می‌شود 2.000000176838287…. ما می‌گوییم که حد این دنباله $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image045.png$ است.

مثال دیگر، دنباله $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image048.png$ است، که جمله Nام آن به این صورت بدست می‌آید: اگر N زوج باشد، عدد قبلی را در $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image049.png$ ضرب، و اگر N فرد باشد، عدد قبلی را در $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image050.png$ ضرب کنید. این دنباله نهایتاً به سمت عدد π همگرا می‌شود. حاصل آخرین کسری که در بالا به آن اشاره شده 2.972154… است (این دنباله خیلی کند همگرا می‌شود). این هم یک دنباله دیگر: $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image051.png$ که اگر آن را ساده کنید می‌شود $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image052.png$ . این دنباله به سمت عدد 2.718281828459 … همگرا می‌شود. این عدد e نام دارد و در ریاضیات از اهمیت بسیار بالایی برخوردار است. من بعداً از این عدد استفاده خواهم کرد.

توجه کنید که همه اینها دنباله‌ای از اعداد هستند که با کاما از یکدیگر جدا شده‌اند. اینها سری نیستند. در یک سری،‌ دنباله‌ای از اعداد با هم جمع می‌شوند. ولی از نقطه نظر آنالیز، یک سری فقط دنباله‌ای است که کمی تغییر قیافه داده. عبارت ”سری $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image053.png$ به 2 همگرا می‌شود“ از نظر ریاضی معادل است با : ”دنباله $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image054.png$ به 2 همگرا می‌شود.“ که در آن دومین جملهِ دنباله برابر است با حاصل جمع دو جمله اول سری، سومین جمله دنباله برابر است با حاصل جمع سه جمله اول سری، و به همین ترتیب. البته به طریق مشابه، گزاره ”دنباله $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image055.png$ واگرا است“ یعنی جمله Nام این دنباله برابر است با جمله قبلی بعلاوه $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image056.png$ .

آنالیز یعنی مطالعه حدود. یعنی چگونه دنباله‌ای از اعداد می‌توانند به یک عددِ مشخص نزدیک و نزدیکتر شوند بدون اینکه هرگز بطور کامل به آن برسند. منظور من از اینکه یک دنباله تا ابد ادامه دارد، این است که هرچقدر هم که این دنباله دارای جمله باشد، من همیشه می‌توانم در ادامه آن یکی دیگر بنویسم. و وقتی می‌گویم حد این دنباله عدد a است، منظورم این است که هر چقدر هم که شما عددی مانند x را کوچک انتخاب کنید، از یک نقطه‌ به بعد، اختلاف تمام اعداد این دنباله از a باز هم از x کمتر است. بجای گزاره‌های فوق شما می‌توانید بگویید ”حد جمله Nام این دنباله هنگامی که N به سمت بی‌نهایت میل می‌کند، a است.“

8.

بطور سنتی ریاضیات به شاخه‌های زیر تقسیم شده است:

§ حساب (Arithmetic): مطالعه اعداد صحیح و کسرها. نمونه‌ای از یک قضیه حساب: اگر شما یک عدد فرد را از یک عدد زوج کم کنید، حاصل همیشه یک عدد فرد است.

§ هندسه (Geometry): مطالعه اَشکال در فضا، یعنی نقاط، خطوط، منحنی‌ها، و اشیاء سه-بعدی. نمونه‌ای از یک قضیه هندسه: مجموع زوایای یک مثلث در یک رویه مسطح، همیشه 180 درجه است.

§ جبر (Algebra): استفاده از علائمِ مجرد برای نمایش اشیاء ریاضی (مثلاً اعداد، خطوط، ماتریس‌ها، تبدیلات، ...)، و مطالعه قواعد ترکیب این علائم. نمونه‌ای از یک قضیه جبر: برای هر دو عددی مثل x و y، همیشه رابطه (x + y) × (x − y) = x² − y² درست است.

§ آنالیز (Analysis): مطالعه حدود. نمونه‌ای از یک قضیه آنالیز: سری هارمونیک واگرا است (یعنی بدون اینکه حدی داشته باشد، افزایش می‌یابد).

البته محتوای ریاضیات نوین بیش از اینها است. مثلاً شامل نظریه مجموعه‌ها (set theory) است که در سال 1874 توسط جورج کانتور ابداع شد. یا منطق ریاضی که توسط ریاضیدان انگلیسی جورج بول ابداع شد، و حالا پایه منطقی کلیه مطالعات ریاضی بر آن قرار دارد. رشته‌های سنتی نیز گسترش یافته‌ تا شامل موضوعات جدید و گسترده‌ باشند. مثلاً هندسه، شامل توپولوژی (topology)، و جبر شامل نظریه بازی‌ها است. حتی پیش از اویل قرن نوزدهم، ما شاهد رسوخ قابل توجه یکی از این حوزه‌ها در دیگری بودیم. مثلاً مثلثات (که لغت آن ابتدا در 1595 مورد استفاده قرار گرفت) هم حاوی عناصری از هندسه و هم جبر می‌باشد. کاری که در واقع دکارت در قرن هفدهم انجام داد حسابی کردن و جبری کردن هندسه بود، هرچند در همان زمان (و نیز امروز) هنوز هم هندسهِ نابِ اقلیدسی، بواسطه وضوح، زیبایی، و نبوغ آن مورد علاقه ریاضیدانان است.

هنوز هم این تقسیم بندی چهارگانه می‌تواند راهنمای خوبی برای شما در جهان ریاضیات باشد. این همچنین راهنمای خوبی برای درک یکی از بزرگترین دست‌آوردهای ریاضیات قرن-نوزدهم است، چیزی که من آن را ”هم‌آمیزی بزرگ“ می‌نامم. این حوزه‌ ترکیبی از مطالعه حساب و آنالیز بود، و حالا ما آن را نظریه تحلیلی اعداد (analytic number theory) می‌نامیم. اجازه دهید در فصل بعد مردی را به شما معرفی کنم که با انتشار یک مقاله هشت و نیم صفحه‌ای نهال نظریه تحلیلی اعداد را برپا ساخت.

فصل 2

خاک و محصول

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image006.png$

28/10/1400

1.

ما چیز زیادی در مورد برنهارت ریمان (Bernhard Riemann) نمی‌دانیم. به غیر از آنچه از نامه‌های ریمان می‌توان استنتاج کرد، او اثری دیگری از زندگی شخصی خودش باقی نگذاشته. دوست و ریاضیدان هم عصر او، ریچارد ددکیند (Richard Dedekind) تنها دوست نزدیک ریمان بود، که از او شرح ‌حالی را نوشته. ولی این تنها شامل 17 صفحه است و چیز زیادی را از زندگی ریمان آشکار نمی‌کند. بنابراین نمی‌توان امیدوار بود که آنچه در دنباله خواهد آمد دربردارنده همه جنبه‌های زندگی ریمان باشد، ولی حداقل امیدوارم در ذهن خواننده چیزی بیش از یک اسم را بجا بگذارد. در این فصل من زندگی دانشگاهی او را بصورت خلاصه بیان می‌کنم، ولی بعداً در فصل 8 آن را با جزئیات بیشتری شرح خواهم داد.

ابتدا اجازه دهید جایگاه او را در زمان و مکانی که می‌زیسته توضیح دهم.

2.

دشمنان فرانسه که خیال می‌کردند انقلاب موجب هرج و مرج و ناکارآمدی در آن کشور شده، به این فکر افتادند تا از این موقعیت استفاده کنند. در سال 1792، نیروی عظیمی از لشکریان اطریش و پروس [2]‌، که شامل 15000 ضدانقلاب فرانسوی بودند، به سوی پاریس پیش‌روی کردند. در کمال تعجبِ نیروهای مهاجم، ارتش انقلابی فرانسه در دهکده والمی با یک ضدحمله که توسط توپخانه انجام داد جلوی آنها را سد کرد. ادوارد کریسی نام این جنگ را نبرد والمی گذاشت. ولی آلمانها به آن توپ‌باران والمی می‌گفتند. نام این جنگ هر چه بود، باعث گشت تا اروپا در طول 23 سال آینده درگیر یک سری از جنگ‌ها شود. معمولاً این رخدادها را جنگ‌های ناپلئونی می‌نامند، ولی با توجه به گستردگی آنها، که هم شامل نبردهایی در آمریکا و هم در خاور دور بود، منطقی‌‌تر است که آنها را اولین جنگ جهانی بنامیم. در 8 ژوئن 1815، هنگامی که سرانجام این جنگ‌ها با انعقاد یک معاهده در وین به پایان رسید، اروپا به یک دوره نسبتاً طولانی از صلح وارد شد، که تقریباً یک قرن طول کشید.

یکی از پیامدهای این معاهده، نظم یافتن جمعیت مردمان ژرمن (آلمانی) در اروپا بود. قبل از انقلاب فرانسه، یک شخص آلمانی زبانِ اروپایی ممکن بود شهروندِ امپراطوری هاپسبورگ اطریش باشد (که احتملاً کاتولیک بود) یا شهروندِ قلمرو پروس (که احتمالاً پروتستان بود)، یا ساکن یکی از سیصد امیرنشینی که در سرزمین آلمان امروزی پراکنده بودند. او همچنین ممکن بود تحت تسلط پادشاه فرانسه؛ یا شاه دانمارک، یا شهروند کنفدراسیون سوئیس باشد. نظمی که به آن اشاره کردم نسبی بود، در آن هنگام آنقدر بی‌نظمی وجود داشت که همیشه موجب جنگ‌های کوچک می‌شد، همان چیزهایی که نهایتاً موجب براه افتادن دو جنگ جهانی در قرن بیستم شدند.

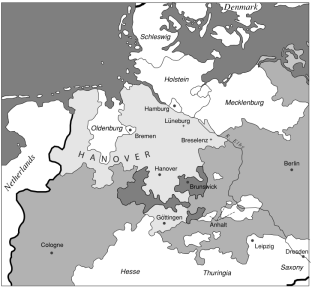
$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image057.png$

شکل 2-1. شمال‌غربی آلمان بعد از 1815. به ایالت هانوفر (Hanover) توجه کنید که به دو قسمت تقسیم شده؛ شهر هانوفر و گوتینگن (Göttingen). پروس (Prussia) به دو قسمت بزرگ و چند قسمت کوچک تقسیم شد؛ هم برلین و هم کُلن جزء شهرهای پروسی هستند. برونسویک (Brunswick) به سه قسمت تقسیم شده.

اطریش هنوز امپراطوری خودش را داشت (که شامل تعداد زیادی از مردم غیر-آلمانی بود: مجارها، اسلاوها، رومانی‌یایی‌ها، چک‌ها، و غیره)؛ سوئیس، دانمارک، و فرانسه نیز مردم آلمان زبان داشتند. ولی عهدنامه وین نقطه شروع خوبی بود. سیصد نهاد مختلف که آلمان قرن هجدهم را تشکیل می‌دادند در 34 ایالت و 4 شهرِ آزاد در هم ادغام شدند، و اتحاد فرهنگی آنها با تشکیل فدراسیون آلمان به رسمیت شناخته شد.

در آن زمان، هنوز هم بزرگترین ایالاتِ آلمانی زبان در اطریش و پروس بودند. جمعیت اطریش 30 میلیون بود، که 4 میلیون آنها آلمان-زبان بودند. پروس 15 میلیون شهروند داشت، که بیشتر آنها آلمان-زبان بودند. خارج از اینها، باواریا (Bavaria) تنها ایالت بزرگ آلمان زبان بود که جمعیتی بیش از 2 میلیون داشت. تنها چهار ایالت بودند که جمعیتی بالای یک میلیون داشتند: هانوفر، ساکسونی، ورتمبرگ، و بادن.

در این میان هانوفر عجیب بود. هرچند این ایالت یک پادشاهی بود، ولی پادشاه آن بندرت در آنجا حضور داشت. زیرا، بنابه دلایل پیچیده‌ای که به دودمان‌های آن موقع ربط داشت، پادشاه هانوفر پادشاه انگلستان نیز بود! چهار نفر اولی که مردم انگلستان آنها را ”پادشاهان هانوفری“ می‌نامیدند، نام همه آنها جورج بود، که چهارمی در سال 1826 تاجگذاری کرد، یعنی در همان زمانی که قهرمان اصلی داستان ”فرضیه ریمان“ متولد شد.

3.

گئورگ فردریش برنهارت ریمان (Georg Friedrich Bernhard Riemann) در 17 سپتامبر 1826 در یکی از دهات قلمرو هانوفر زاده شد. این بخش وِندلند (Wendland) نامیده می‌شد. در آلمان قدیم، لغت وِند (Wend) برای اشاره به مردمان اسلاو-زبان بکار برده می‌شد. وِندلند دورترین منطقه غربی بود که قوم اسلاو در قرن ششم به آنجا هجوم بردند. هنوز هم در آنجا گویش و رسوم اسلاوها بجا مانده. فیلسوف و ریاضیدان آلمانی، لایب‌نیتز (1716- 1646) در مورد فرهنگ آنها تحقیقات زیادیی را انجام داد. ولی از اواخر قرون وسطی به بعد، مهاجرین آلمان-زبان به وندلند نقل مکان کردند، طوری که در زمان ریمان جمعیت آنجا را اکثراً آلمانها تشکیل می‌دادند.

در آن زمان وندلند جای عقب‌مانده‌ای بود، و هنوز هم نسبتاً چنین است. امروز وِندلَند در ایالت ساکسونی سُفلی (Lower Saxony) قرار دارد، و با داشتن جمعیت 110 نفر در هر مایل مربع، کمترین تراکم جمعیت را در این ایالت دارد. صنایع اندکی در آنجا وجود دارد.

پدر ریمان، که نام او نیز برنهارت بود، یک کشیش لوتری و یک کهنه سرباز جنگ‌های ناپلئونی بود. هنگامی که او با مادر ریمان، شارلوت، ازدواج کرد، او مرد میان‌سالی بود. برنهارت فرزند دوم آنها بود، و بنظر می‌رسد به خواهر بزرگش، ایدا، نزدیک بود، و به همین دلیل بعدها نام دختر خودش را نیز آیدا گذاشت. ریمان بعداً صاحب یک برادر و سه خواهر دیگر نیز شد. همه ما قبول داریم که با استانداردهای زندگی امروز، مشکل می‌توان سختی‌هایی که یک مرد روستایی میان‌ سال برای پشتیبانی از همسر و شش فرزند خودش داشت را تصور کنیم، آن هم در قرن نوزدهم و در یک ناحیه فقیر و دورافتاده. از میان پنج خواهر و برادر ریمان، تنها کسی که بطور طبیعی عمر کرد خواهر بزرگش آیدا بود. بقیه آنها در جوانی فوت کردند، که احتمالاً دلیل آن سوء تغذیه بود. مادر ریمان نیز پیش از اینکه بچه‌هایش بزرگ شوند در جوانی درگذشت.

در آن دوران و شرایط، گذشته از فقر، یافتن کار نیز بسیار مشکل بود. به سختی می‌شد طبقه متوسط را خارج از شهرهای بزرگ پیدا کرد. در آن ناحیه، اشخاصی مثل تُجار، روحانیان، معلمین، دکترها، و کارمندان دولتی بصورت پراکنده زندگی می‌کردند. هر کس دیگری که مالک زمین نبود، یا صنعتگر بود یا روستایی. تنها شغل آبرومندانه‌ای که برای یک زن وجود داشت خدمت‌کاری خانه دیگران بود؛ در غیر اینصورت آنها برای پشتیبانی خودشان به شوهر یا یکی از اعضای ذکور خانواده متکی بودند.

هنگامی که برنهارت هنوز یک بچه بود، پدرش بعنوان یک کشیش شغلی را در کویک‌بورن (Quickborn) برگزید. امروز هم کویک‌بورن یک دهکده بی‌سروصدا با خانه‌هایی است که از الوار ساخته شده‌اند و خیابان‌هایی دارد که دو طرف آن با درختان بلوط پوشیده شده، و بیشتر آنها هنوز آسفالت نشده‌اند. تا زمانی که پدر ریمان در سال 1855 فوت کرد، خانه آنها در آنجا بود. تا وقتی ریمان به سن 30 سالگی نرسیده بود، مرکز دنیای عاطفی او را این مکان تشکیل می‌داد. بنظر می‌رسید که او از هر فرصتی استفاده می‌کرد تا به آنجا باز گردد، و در میان خانواده خودش باشد، جایی که او همیشه در آن احساس آرامش می‌کرد.

بنابراین، اگر کسی سرگذشت ریمان را می‌خواند، باید این شرایط و محیط را در نظر بگیرد؛ محیطی که او در آن تربیت یافت برایش عزیر بود، و هنگام دوری از آنجا، دلتنگ می‌شد. دهکده‌ای نمناک با خانه‌ای بادگیر که تنها با شمع و روغن چراغ روشن می‌شد، و در زمستان‌ بسیار سرد، و در تابستان گرم بود؛ خانه‌ای که برای مدت درازی با بیماری احاطه شده بود (و بنظر می‌رسید که همه اعضای خانواده از مرض سل رنج می‌بردند)؛ زندگی ساده و یکنواخت در یک خانواده کشیش در یک دهکده دورافتاده؛ رژیم غذایی ناکافی و نامتوازن (او برای مدت‌ها از یبوستِ مزمن رنج می‌برد). تحمل چنین زندگی چگونه میسر بود؟ ولی آنها می‌دانستند که برای تحمل سختی‌ها، هیچ چیزی جزء علاقه و محبت نمی‌تواند روح انسان را پابرجا نگاه دارد.

4.

در زمان ریمان، اکثر ایالاتی که شمال آلمان را تشکیل می‌دادند (یعنی پادشاهی‌ها، امیرنشین‌ها، و دوک‌نشین‌ها) بطور عمده از یکدیگر مستقل بودند و هر کدام سیاستهای داخلی خودشان را داشتند. این ساختارِ سست، موجب غرورِ محلی و رقابت میان ایالات بود.

آنها در بسیاری موارد از پروس رهنمود می‌گرفتند. بخش شرقی آن قلمرو، تنها ایالت آلمان بود که بعد از شکست در مقابل ناپلئون (1807-1806) توانسته بود تا حدی استقلال خودش را حفظ کند. تحت تاثیر آن معاهده، پروسی‌ها تمرکز خودشان را روی اصلاحات داخلی گذاشتند، و زیر نظر زبان‌شناس و فیلسوفی بنام ویلهلم هومبولت (Wilhelm Humboldt) نظام آموزشِ متوسطه خودشان را دوباره بازسازی کردند. هومبولت یک شخصِ سُنتی و کمالگرا بود. او یکبار گفته بود ”من از هر آنچه جدید است بیزارم“. با اینحال، همین اصلاحاتِ آموزشی سخت و عبوس، نهایتاً باعث شد دستگاه آموزشی ایالاتِ آلمان به پیشرفته‌ترین نوع خودشان در اروپا بدل شوند.

در محور این دستگاه آموزشی، یک دوره 10-ساله دبیرستانی قرار داشت، که دانش‌آموزان از 10 تا 20 سالگی در آن تحصیل می‌کردند. در دوره‌های نخست، مواد آموزشی این دبیرستان‌ها به موارد زیر تقسیم می‌شدند:

زبان لاتین %25

زبان یونانی 16%

زبان آلمانی 15%

ریاضیات 20%

تاریخ و جغرافی 10%

علوم 7%

دینی 7%

در مقابل، بر طبق گزارش‌هایی که از برنامه‌های آموزشی دهه 1840 انگلستان در دسترس است، 75 تا 80 درصد به دروس غیر علمی اختصاص یافته بود.

دهکده کویک‌بورن دبیرستان نداشت و ریمان تا 14 سالگی به طور مرتب به مدرسه نرفته بود. برای اینکه به دبیرستان برود، باید به پایتخت ایالت، یعنی هانوفر می‌رفت که 130 کیلومتر از کویک‌بورن فاصله داشت. تنها مزیتی که برای او وجود داشت این بود که پدربزرگش در هانوفر زندگی می‌کرد و او مجبور نبود هزینه یک مدرسه شبانه‌روزی را پرداخت کند. پیش از اینکه به دبیرستان برود، پدرش با کمک یکی از معلمان دهکده بنام آقای شولتز، آموزش‌هایی را به او داده بود.

هنگامی که ریمانِ 14 ساله در هانوفر بسر می‌برد، خیلی غمگین و ناراحت بود، و به طرز عجیبی خجالتی و همیشه دلتنگ خانه بود. تنها فعالیتی که ما از آن اطلاع داریم و او خارج از برنامه درسی خودش انجام می‌داد، بیرون رفتن و تلاش برای خرید هدایا برای افراد خانواده خودش بود، تا این هدایا را به مناسبت تولد به خانه بفرستد. مرگ پدربزرگش در 1842 باعث بهبودی اندکی در زندگی او شد. ریمان را به دبیرستان دیگری فرستادند که در شهر لون‌بُرگ قرار داشت. ددکیند دراینباره چنین می‌نویسد:

نزدیکی بیشتر به خانه، فرصتی برای او فراهم می‌‌کرد تا بتواند تعطیلات را در کنار خانواده‌اش باشد، و این باعث شد تا زندگی او نسبت به قبل بسیار شادتر شود. مسلماً این رفت و آمدهای طولانی که بیشتر با پای پیاده انجام می‌‌گرفت از نظر جسمی بسیار خسته کننده بودند، و او به آنها عادت نداشت. در نامه‌‌هایی که مادرش برای ریمان می‌نوشت، و اظهار می‌‌داشت مریض است و بزودی می‌‌میرد، همشه نگران سلامتی او بود و به وی نصیحت می‌‌کرد از نظر جسمی خیلی تقلا نکند.

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image058.png$

ریچارد ددکیند، ریاضیدان، و دوست ریمان (Richard Dedekind)

بنظر نمی‌‌رسید که ریمان دانش‌‌آموز ممتازی باشد. ذهن او طوری بود که فقط می‌‌توانست چیزهایی را در خودش نگاه دارد که برای او جالب بود، و این عمدتاً شامل ریاضیات می‌‌شد. بعلاوه، او یک شخصِ کمال‌‌گرا و باوجدان بود که عقیده داشت نوشتن یک انشاء بی‌‌نقص اهمیت بیشتری دارد تا سریع نوشتن آن. برای بهبود وضعیت ریمان، مدیر مدرسه تصمیم گرفت که او را به معلمی که عبری درس می‌‌داد معرفی کند. تحت راهنمایی‌‌های این شخص، دروس عمومی ریمان آنقدر خوب شد که در سال 1846 برای ورود به رشته الهیات دانشگاه گوتینگن پذیرش گرفت. هدف آن بود که او بتواند راه پدر را دنبال کرده و کشیش شود.

5.

گوتینگن تنها دانشگاهی بود که در نزدیکی کلیسای هانوفر قرار داشت، بنابراین رفتن به آنجا منطقی بود. در این کتاب بارها از ” گوتینگن“ نام برده خواهد شد، بنابراین بد نیست چند کلمه‌‌ای هم از تاریخ آنجا یاد کنیم. این دانشگاه در سال 1734 توسط جورج دوم پادشاه انگلستان (که امیر هانوفر نیز محسوب می‌‌شد) بنا نهاده شد، و با داشتن بیش از 1500 دانشجو در 1823، سریعاً به یکی از بهترین دانشگاه‌‌های آلمان بدل گشت.

ولی دهه 1830 دوران پر دردسری بود. اضطرابات سیاسی که هم توسط دانشجویان و هم توسط استادان بوجود آمده بود، باعث شد تا در 1834 تعداد دانشجویان به 900 نفر کاهش یابد. سه سال بعد، مشکل به اوج خودش رسید، و باعث شد گوتینگن در کل اروپا معروف شود. ویلیام چهارم، که هم پادشاه انگلستان و هم هانوفر بود، درگذشت و برادرزاده‌‌اش ویکتوریا جانشین او شد. ولی هانوفر که به سنتها و قوانین قرون وسطایی پای‌بند بود، فقط اجازه میداد فرزندان ذکور به سلطنت برسند. درنتیجه راه انگلستان و هانوفر از یکدیگر جدا شد. ارنست آگوستوس، که یکی از فرزندان جورج سوم بود، حاکم جدید هانوفر شد.

ارنست آگوستوس یک مرتجع کامل بود. اولین اقدام او کنارگذاشتن قانون اساسی آزادی‌خواهانه‌ای بود که چهار سال قبل ویلیام چهارم آن را پایه‌گذاری کرده بود. هفت استاد دانشگاه گوتینگن از سوگند به قانون اساسی جدید امتناع ورزیدند، و به همین دلیل اخراج شدند. در واقع سه نفر از آنها از هانوفر تبعید شدند. این استادان اخراجی، که به ”هفت یار گوتینگن“ معروف شدند، برای اصلاح‌طلبان سیاسی و اجتماعی سراسر اروپا مانند قهرمان بودند. از میان آنها می‌توان به برادران گریم (Grimm) اشاره کرد که هر دو زبان‌شناس بودند و برای نوشتن کتاب ”داستان‌های عامیانه“ معروف هستند.

به دنبال تغییرات فاحشی که در 1848 در سراسر قاره اروپا پدید آمد، هانوفر نیز یک قانون اساسی آزادی‌خواهانه کسب کرد. حداقل یکی از هفت یار گوتینگن، که فیزیکدانی بنام ویلهلم وبر (Wilhelm Weber) بود، دوباره به کار منصوب شد. دانشگاه دوباره به شکوه خودش بازگشت، و همانطور که خواهیم دید، نهایتا به یکی از مراکز بزرگ آموزشی جهان تبدیل شد. ولی هنگامی که برنهارت ریمان در سال 1846 به آنجا وارد شد، هنوز تحولات کامل نشده بود. در ابتدا گوتینگن برای ریمان جای راحتی نبود، و به دلیل اعتراضات 9 سال قبل، دانشگاه هنوز درحال بهبودی بود.

با اینحال گوتینگن برای ریمان جوان یک جذابیت عمده داشت. این دانشگاه خانه بزرگترین ریاضیدان دوران خودش (و شاید کل دوران‌ها)، کارل فردریش گاوس (Carl Friedrich Gauss) بود.

هنگامی که ریمان به گوتینگن وارد شد گاوس 69 ساله بود. او بهترین دوران کاریش را پشت سر گذاشته بود و کمتر تدریس می‌کرد، و آن را اتلاف وقت می‌دانست. بااینحال، ریمان که از قبل شیفته ریاضیات شده بود، تحت تاثیر حضور گاوس قرار گرفت. ما می‌دانیم که ریمان در درس‌های جبرِ خطی گاوس و نظریه معادلات موریتز استرن (Moritz Stern) شرکت می‌کرد. ولی در طول این سال (1847-1846)، ریمان باید دو دل شده باشد که آیا الهیاتی که پدرش می‌خواست، یا ریاضیاتی که خودش به آن دلبسته بود را دنبال کند. نهایتاً پدرش که مرد مهربانی بود رضایت داد که او ریاضیات را بعنوان شغل خودش برگزیند. به این ترتیب، ریمان ریاضیدان شد.

6.

از شخصیتِ بالغ ریمان اطلاعات کمی به ما رسیده. منبع اصلی که دراینمورد وجود دارد، همان خاطرات کوتاه ددکیند است که در ابتدای این فصل به آن اشاره کردم. این خاطرات 10 سال پس از مرگ ریمان نوشته شده و ضمیمه کتابِ آثار منتخب او شده بود (ولی تا آنجا که می‌دانم هیچ وقت به انگلیسی ترجمه نشده). من در نوشتن کتاب حاضر، از مطالب کتاب مذکور خیلی استفاده کردم، طوری که بسیاری از مطالبی که در اینجا و فصل 8 آورده شده در واقع باید به این صورت نقل قول می‌شد: ”بر طبق گفته ددکیند، ...“. البته باید توجه داشت که گرچه ددکیند نزدیکترین دوست ریمان بود، ولی او نیز می‌تواند در بیان حقایق اشتباه کرده باشد. ددکیند مرد صادق و درستکاری بود و جز یک مورد که بعداً به آن اشاره خواهم کرد، هیچ وقت مطلبی را ندیدم که برخلاف این دلالت کند. منبع دیگری که وجود دارد نامه‌های خصوصی ریمان هستند که بسیاری از آنها باقی مانده‌اند. البته اظهار نظرهای شاگردان و همکاران او نیز موجودند.

همه اینها حالی از موارد زیر هستند:

· ریمان مرد فوق‌العاده محجوبی بوده. او تا حد ممکن از تماس با بقیه پرهیز می‌کرده، و در همراهی با دیگران مشکل داشته. تنها کسانی که به آنها نزدیک بود، یکی خانواده او (و آنها حقیقتاً به هم نزدیک بودند)، و پس از آنها، فقط ریاضیدانان دیگر، بودند. هنگامی که میان خانواده خودش در کویک‌بورن نبود، از دلتنگی آنها رنج می‌برد.

· او به سبکِ یک آلمانی پروتستان، بسیار مومن بود. او معتقد بود که اساسِ دین ”آزمون روزانه در پیشگاه خداوند است“ (بطور تحت‌الفظی از کتاب آلمانی ددکیند ترجمه کرده‌ام).

· او بطور عمیق درباره فلسفه می‌اندیشید و همه کارهای ریاضی خودش را در قالب یک فلسفه بزرگتر می‌دید.

· او به معنای واقعی کلمه، افسرده (hypochondriac) بود. البته به خاطر اصرار بیوه ریمان مبنی بر پنهان ماندن افسردگی او، ددکیند از بکاربردن این کلمه پرهیز می‌کرد. بااین وجود، ددکیند بطور صریح گفته بود که ریمان از یک غمِ عمیق رنج می‌برد، خصوصاً بعد از مرگ پدرش، که او را بسیار دوست می‌داشت، ریمان برای تسکین خودش، غرق در کار شد.

· وضعیت سلامت او هیچگاه خوب نبود و همیشه از یک بیماری رنج می‌برد.

گاهی ما وسوسه می‌شویم تا ریمان را بیشتر یک آدم مغموم و تا اندازه‌ای رقت‌انگیز فرض کنیم. ولی همه اینها جنبه‌های بیرونی شخصیت او بود. در درون آن شخصیتِ محجوب و در خود رفته، ذهنی قرار داشت با حداکثر نبوغ و استعداد که به طرز حیرت‌انگیزی بی‌پروا بود. از دید یک رهگذر عادی، هر چقدر ظاهر ریمان بی‌حال و کم‌رو بنظر می‌آمد، ریاضیات او، مانند نبردهای ناپلئون، پهناور و بی‌باک بود.

زندگی ریمان مرا یاد کتاب ”ماه و شش پنی“ نوشته سامرست موآم می‌اندازد، که از زندگی نقاش فرانسوی پُل گوگن الهام گرفته. قهرمان کتابِ موآم نیز مانند گوگنِ نقاش، به کلبه‌ای در یکی از جزایر اقیانوس آرام پناه می‌برد تا هنر خودش را دنبال کند، و در همانجا از مرض جذام می‌میرد. دکتر دهکده که خبردار می‌شود او درحال مرگ است به کلبه او می‌رود. کلبه‌ای مخروب و محقر. ولی هنگامی که دکتر پا به کلبه می‌گذارد، با کمال تعجب می‌بیند که تمام دیوارهای داخلی، از کف گرفته تا سقف، با نقاشی‌های درخشان و شگفت‌انگیزی رنگ‌آمیزی شده‌اند. ریمان نیز مانند این کلبه بود. از بیرون قابل‌ترحم بود، ولی از درون چنان می‌سوخت که از خورشید هم درخشان‌تر بود.

7.

اصلاحاتی که فون هومبولت در زمینه تحصیلات عالی بعمل آورد، فقط در برلین پایتخت پروس قابل مشاهده بود. هنریش وبر در مقدمه‌ای که بر کتاب آثار منتخب ریمان نوشته، وضعیت بقیه دانشگاه‌های آلمان را اینطور توصیف می‌کند:

پشتیبانانِ سخاوتمندِ دانشگاه‌ها فکر می‌کردند که هدف از دانشگاه‌ تربیت وکلا، پزشکان، معلمین، واعظین، و همچنین جایی برای پسران نجبا و ثروتمندانی بود که در آنجا بتوانند اوقات خودشان را به خوشی و احترام سر کنند.

در واقع، اصلاحات هومبولت تا مدتی تاثیر منفی بر تحصیلاتِ عالی آلمان گذاشته بود. این باعث افزایش تقاضا برای معلمینِ آموزش دیده دبیرستان شد، و تنها راه برآورده شدن این تقاضا این بود که دانشگاه‌ها درگیر تربیت آنها شوند. حتی گاوسِ کبیر نیز در دانشگاه گوتینگن بیشتر وقت خودش را صرف تدریس دوره‌های مقدماتی می‌کرد (1847-1846). ریمان برای گذراندن درس‌های پیشرفته‌تر به دانشگاه برلین رفت. او در آنجا دو سال زیر نظر بهترین ریاضیدانان آلمان پرورش یافت، و به یک ریاضیدان کاملاً پخته بدل گشت.

خواننده باید توجه داشته باشد که پیش از دوره ناپلئون، نگاهی که به نهادِ دانشگاه وجود داشت بر دو قسم بود؛ در یک سمت دانشگاه‌هایی قرار داشتند که هدف عمده آنها تعلیم و تربیت دانشجو بود، و در سوی دیگر، آکادمی‌ها یا انجمن‌ها بودند، که هدف آنها تحقیق بود، تحقیقاتی که ماهیت آنها به زمان خودشان و یا تمایلات رهبران کشورها بستگی داشت. موسساتی مانند دانشگاه برلین، که در سال 1810 تاسیس شد، در این میان استثنا بودند، زیرا اندکی تحقیق نیز در آنجا صورت می‌گرفت. ولی اولین جایی که فرضیه ریمان در آنجا مطرح شد، آکادمی برلین بود که یک موسسه کاملاً تحقیقاتی بود که از روی انجمن سلطنتی انگلستان الگو برداری شده بود.

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image059.png$

برنهارت ریمان در اوایل دهه 1850

تنها چیزی که ما از زندگی روزمره ریمان در برلین می‌دانیم، مطالعاتِ ریاضی اوست. در یادداشت‌های ددکیند تنها یک نکته قابل ذکر دیده می‌شود. در ماه مارس 1848، جمعیتی در برلین گرد هم آمدند، و با الهام از انقلاب فوریه پاریس، با اشغال خیابان‌ها خواستار اتحاد ایالات آلمان در یک امپراتوری واحد شدند. سنگرها به پا شدند، ارتش برای پاکسازی آنها اعزام شد، و خون ریزی شروع شد. در آن زمان فردریک ویلهلم چهارم شاهِ پروس بود، فردی ساده و رویاپرداز، که بیشتر تحت تاثیر جنبش‌های شاعرانه بود. او نسبت به مردم یک دیدگاه احساساتی داشت، و به کشورِ ایدآلی معتقد بود که بر اساس یک سلطنتِ پدرسالارانه قرار داشته باشد. او در برخورد با این بحران، ناشیانه رفتار کرد. او ارتش را به اردوگاه بازگرداند و پیش از این که شورشیان متفرق شوند، بدون محافظ قصر خودش را ترک کرد. دانشجویان دانشگاه برای محافظت از پادشاه فوجِ نگهبانان وفادار را تشکیل دادند، و ریمان از ساعت 9 صبح، تا ساعت 1 بعد از ظهرِ روز بعد، کلاً برای 28 ساعت نگهبانی داد.

ریمان بعد از بازگشت به گوتینگن در سال 1849، کار روی تز دکترای خودش را شروع کرد، که دو سال طول کشید، و در سن 25 سالگی رساله خودش درباره نظریه توابع مختلط را ارائه کرد. او سه سال بعد در گوتینگن مُدرس، و در سال 1857 استادیار شد، که اولین منصبی بود که با حقوق همراه بود (در آن زمان مدرسین دانشگاه تنها از دانشجویانی حق‌التدریس می‌گرفتند که درس‌هایشان برای آنها جذاب بود، و به آنها مُدرس خصوصی می‌گفتند). سال 1857 ”سال شکوفایی“ ریمان نیز بود. رساله دکترایش، که در سال 1851 منتشر شد، حالا یک اثر کلاسیکِ ریاضیِ قرن ‌نوزدهمی محسوب می‌شود، ولی علی‌رغم تحسین‌های زیاد گاوس، کسی زیاد به آن توجهی نشان نداد. مقالاتی که او در اوایل دهه 1850 نوشته بود، خیلی معروف نشدند، و تنها پس از مرگش منتشر و در دسترس قرار گرفتند. معروفیت او در آن زمان بیشتر بخاطر محتوای درس‌هایی بود که ارائه می‌داد؛ و بیشتر آنها چنان از زمان خودش جلوتر بودند که کمتر کسی ارزش آنها را می‌فهمید. ولی در سال 1857 ریمان مقاله‌ای را درباره آنالیز منتشر کرد که فوراً ارزش آن شناخته شد و همه معترف بودند که سهم بزرگی را در این رشته داشته است. عنوان این مقاله ” نظریه توابع آِبلی“ بود. او در آنجا با روش‌های نوآورانه و نبوغ‌آمیز خودش به حل مسائل آن حوزه پرداخت. ظرف مدت یکی دو سال، نام ریمان برای ریاضیدانان سراسر اروپا شناخته شده بود. او در سال 1859 به سمت استاد تمامی دانشگاه گوتینگن ارتقاء یافت. حالا او آنقدر درآمد داشت که بتواند ازدواج کند، و سه سال بعد اینکار را انجام داد. همسر او یکی از دوستان خواهر بزرگش بنام الیزه کوخ بود.

در 11 آگوست 1859، چند روز پیش از تولد 33 سالگی‌اش، برنهارت ریمان به عضو افتخاری آکادمی برلین انتخاب شد. تصمیم آکادمی تنها براساس دو مقاله شناخته شده ریمان اتخاذ شده بود؛ یکی رساله دکترای او در 1851، و دیگری مقاله 1857 درباره نظریه توابع آِبلی. عضویت در آکادمی برلین برای یک ریاضیدان جوان افتخار بزرگی بود. در پاسخ به چنین انتصابی، آن زمان رسم بود که شخص انتخاب شده مقاله‌‌ای را به آکادمی تسلیم کند که حاوی تحقیقاتِ جاری او باشد. عنوان مقاله‌ای که ریمان به آکادمی تسلیم کرد ”در باب تعداد اعداد اول کمتر از یک کمیت مفروض“ بود.

از آن زمان به بعد، ریاضیات دیگر آن ریاضیات سابق نبود.

فصل 3

قضیه اعداد اول

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image006.png$

02/11/1400

1.

خوب، پیش از یک عدد مفروض، چه تعداد اعداد اول وجود دارند؟ من بزودی پاسخ این سئوال را به شما خواهم گفت، ولی ابتدا پنج دقیقه وقت می‌خواهم تا درباره اعداد اول (prime numbers) توضیح دهم.

یک عدد صحیحِ مثبت، مثل 28 را در نظر بگیرید. دقیقاً چه اعدادی بر آن بخش‌پذیرند؟ جواب عبارت است از: 1, 2, 4, 7, 14, و خود28 . اینها عوامل یا فاکتورهای (factors) عدد 28 هستند. بنابراین ما می‌گوییم ”28، شش عامل دارد.“

عدد 1 عاملِ تمام اعداد است، و هر عددی عامل خودش نیز هست. ولی اینها عامل‌های خیلی جالبی نیستند. ما در ریاضیات به این عامل‌ها، عوامل بدیهی یا بی‌مایه (trivial) می‌گوییم. عامل‌های جالب 28، اعداد 2، 4، 7، و 14 هستند. این عوامل، عوامل حقیقی (proper) نامیده می‌شوند.

بنابراین عدد 28 دارای چهار عامل حقیقی است. ولی عدد 29 هیچ عاملِ حقیقی ندارد. این عدد به غیر از 1 و خود 29 بر هیچ عدد دیگری بخش‌پذیر نیست. اینها اعداد اول (prime number) نامیده می‌شوند. پس یک عدد اول، عددی است که هیچ عامل حقیقی ندارد. در زیر اعداد اول کوچکتر از 1000 را می‌بینید:

2 3 5 7 11 13 17 19 23 29 31 37 41 43

47 53 59 61 67 71 73 79 83 89 97 101 103 107

109 113 127 131 137 139 149 151 157 163 167 173 179 181

191 193 197 199 211 223 227 229 233 239 241 251 257 263

269 271 277 281 283 293 307 311 313 317 331 337 347 349

353 359 367 373 379 383 389 397 401 409 419 421 431 433

439 443 449 457 461 463 467 479 487 491 499 503 509 521

523 541 547 557 563 569 571 577 587 593 599 601 607 613

617 619 631 641 643 647 653 659 661 673 677 683 691 701

709 719 727 733 739 743 751 757 761 769 773 787 797 809

811 821 823 827 829 839 853 857 859 863 877 881 883 887

907 911 919 929 937 941 947 953 967 971 977 983 991 997

همانطور که می‌بینید تعداد آنها 167 عدد است. در اینجا ممکن است کسی اعتراض کند و بگوید چرا عدد 1 در این فهرست، یا هر فهرست دیگری از اعداد اول، نیامده. مگر نه اینکه 1 در تعریف اعداد اول صدق می‌کند؟ خوب، اگر بخواهید خیلی دقیق صحبت کنید، جواب مثبت است و برای خشنودی خودتان می‌توانید ”1“ را به فهرست اعداد اول اضافه کنید. ولی شامل کردن 1 در فهرست اعداد اول دردسر آفرین است، و امروزه ریاضیدانان طبق یک توافق عمومی اینکار را نمی‌کنند (آخرین ریاضیدان معروفی که اینکار را کرد، هنری لُبگ Henri Lebesgue در سال 1899 بود). درواقع، حتی گنجاندن 2 در این فهرست نیز کار بیهوده‌ای است. تعداد بی‌شماری از قضایا هستند که با عبارتی نظیر ”فرض کنید p یک عدد فرد اول باشد ...“ شروع می‌‌شوند، و تکلیف 2 را مشخص می‌‌کند. ولی به هر حال، 1 را جزئی از این فهرست نمی‌‌دانند.

اگر بطور دقیق به فهرست اعداد اول نگاه کنید، خواهید دید که هر چقدر جلو می‌روید تعداد آنها کمتر می‌شود. بین اعداد 1 تا 100 بیست و پنج عدد اول قرار دارند؛ بین اعداد 401 تا 500 هفده عدد؛ و بین اعداد 901 تا 1,000 تنها 14 عدد اول قرار دارند. بنظر می‌رسد که هر چه جلو می‌رویم، تعداد اعداد اول موجود در بلوک‌های 100تاییِ اعدادِ صحیح کاهش می‌یابد. اگر شما همین رویه را دنبال کنید و به آخرین بلوک اعداد صدتایی کوچکتر از یک میلیون نگاه (اعداد میان 999,901 تا 1,000,000) خواهید دید که در میان آنها تنها 8 عدد اول وجود دارد. و اگر همین کار را برای آخرین بلوک صدتایی کوچکتر از یک تریلیون تکرار کنید، تنها 4 عدد اول را خواهید دید که اینها هستند:

999,999,999,937; 999,999,999,959; 999,999,999,961; و 999,999,999,989

2.

با توجه به موارد فوق، طبیعتاً این سئوال پیش می‌آید که آیا هر چه جلوتر می‌رویم تعداد اول کاهش می‌یابد و نهایتاً به صفر می‌رسد؟ اگر من همین کار را برای فهرست اعداد اول موجود در آخرین بلوک صدتایی یک تریلیون تریلیون، یک تریلیون تریلیون تریلیون تریلیون انجام دهم، آیا به نقطه‌ای خواهم رسید که دیگر عدد اولی وجود نداشته باشد؟ به عبارت دیگر، آخرین چیزی که در فهرست من قرار گرفته، بزرگترین عدد اول باشد؟

پاسخ این سئوال حدود 300 سال پیش از میلاد توسط اقلیدُس داده شد. فهرست اعداد اول هیچگاه به پایان نمی‌رسد، و همیشه اعدادِ اولِ بیشتری وجود خواهند داشت. هیچ عدد اولی نیست که بزرگتر از بقیه باشد. هر عدد اولی را که پیدا کنید، هر چقدر هم که بزرگ باشد، همیشه عدد اول دیگری وجود دارد که از عدد شما بزرگتر باشد. فهرست اعداد اول تا ابد ادامه دارد. اثبات: فرض کنید که N یک عدد اول باشد. حاصل عدد زیر را پیدا کنید:

(1 × 2 × 3 × … × N) + 1

عدد فوق بر هیچ یک از اعداد کوچکتر از 1 تا N بخش پذیر نیست (این عدد را بر هر یک از اعداد 1 تا N که تقسیم کنید، باقیمانده 1 خواهد بود). بنابراین، این عدد یا هیچ عامل اولی ندارد (که یعنی خود این عدد یک عدد اول است)، و یا عامل اول آن از N بزرگتر است. بدلیل اینکه عواملِ اول یک عدد همیشه از خود عدد کوچکترند، این قضیه ما را اثبات می‌کند. مثلاً اگر N=5 باشد، 1×2×3×4×5+1=121، که کوچکترین عامل اول آن 11 است (11>5). شما از هر عدد اولی که شروع کنید، به عدد اولِ بزرگتری خواهید رسید. (من بعداً در بخش 4 فصل 7، پس از شرح ” کلید طلایی“، اثبات دیگری برای بی‌نهایت بودن تعداد اعداد اول ارائه خواهم داد.)

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

فصل 4

بر روی شانه غول‌ها

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image006.png$

02/11/1400

1.

اولین شخصی که صحت قضیه اعداد اول (ق.ا.ا) به فکرش رسید، کارل فردریش گاوس (Carl Friedrich Gauss) بود. همانطور که در قسمت 5 فصل 2 گفتم، ادعا می‌شود که گاوس بزرگترین ریاضیدانی است که تاکنون زیسته. او در زمان خودش به شاهزاده ریاضیات معروف بود، و هنگامی که فوت کرد، جورج چهارم، پادشاه هانوفر فرمان داد تا به افتخار او مدالی ساخته، و عنوان شاهزاده ریاضیات روی آن حک شود.

گاوس از خوانواده بسیار فقیری می‌آمد. پدربزرگ او یک روستایی بود که زمینی نداشت؛ پدرش یک باغبان بود که گاهی اوقات خشت‌مالی می‌کرد. گاوس به فقیرترین مدرسه‌ آنجا می‌رفت. در مورد گاوس حکایتی نقل می‌شود که به احتمال زیاد حقیقت دارد. روزی معلم مدرسه که می‌خواسته به خودش استراحتی بدهد، تصمیم می‌گیرد به شاگردان بگوید که اعداد 1 تا 100 را با هم جمع کنند. همان موقع گاوس فوراً لوح خود را روی میز معلم می‌گذارد، و می‌گوید ”حل کردم!“. کاری که گاوس در ذهنش انجام داده بود این بود که اعداد را در دو سطر مرتب کرده بود، یکی بصورت عادی و دیگری بصورت معکوس:

1, 2, 3, … 100

100, 99, 98, … ,1

و سپس این دو سطر را با هم جمع کرده بود:

(101, 101, 101, …, 101)

که می‌شود 100×101 و بدلیل اینکه همه اعداد 2 بار ظاهر شده بودند، باید نتیجه را تقسیم بر 2 کرد، که می‌شود 5,050. به قول معروف، چو مسئله حل شود، آسان شود! ولی نه برای یک پسربچه 10 ساله؛ و نه حتی برای یک فرد 30 ساله.

از بخت خوب گاوس، معلمش به توانایی‌های او پی برد و به او کمک کرد تا آنها را ارتقاء دهد. و حتی خوش‌شانسی بزرگ او این بود که در دوک‌نشین کوچک برونزویک زندگی می‌کرد. برونزویک توسط کارل ویلهلم فردیناند، که ملقب به دوکِ برونزویک بود، اداره می‌شد. ما قبلاً در فصل 1 با این دوک آشنا شدیم. او در سراسر زندگی خودش یک سرباز غیور بود، و در ارتش پروس درجه فیلد مارشالی داشت، یعنی فرمانده کل نیروهای ارتش پروس، که فرانسه آنها را در 1792 در نبرد والمی متوقف کرده بود.

کارل ویلهلم حقیقتاً مرد نجیبی بود. اگر جایی بنام بهشتِ ریاضی‌دانان وجود داشته باشد، به پاس خدمات کارل ویلهلم، باید عمارت مهمی را برای او در آنجا نظر گرفت. دوک که از استعداد گاوس باخبر شده بود، از او خواست که به دیدارش برود. در آن زمان گاوس زیاد با آداب معاشرت آشنا نبود. بعدها، به علت راه‌یابی به دربارِ پادشاهان و دانشگاه‌ها، دیگران او را بعنوان یک فرد آرام و مهربان توصیف کرده‌اند؛ ولی او همیشه چهره‌ای زمخت و قامت یک روستایی اصیل را داشت. ولی دوک آنقدر بصیرت داشت که سیمای واقعی او را ببیند. از آن زمان به بعد، دوک چنان درآمدی را برای او فراهم آورد که تا وقتی زنده بود گاوس توانست به مدت طولانی بعنوان یک ریاضیدان، فیزیکدان و منجم فعالیت‌های درخشان خودش را دنبال کند.

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image060.png$

کارل ویلهلم فردیناند حامی گاوس

پشتیبانی دوک از گاوس بشکل غم‌انگیزی پایان یافت. در 1806 ناپلئون در اوج قدرت قرار داشت. در نبردهایی که سال قبل انجام داده بود، او توانسته بود ارتش متحد روسیه و اطریش را در نبرد استرلیتز (Austerlitz) شکست دهد، و با اهداء موقتِ هانوفر به پروسی‌ها، توانسته بود آنها را بخرد. سپس او هم‌پیمانی راین را تاسیس کرد، و کلیه بخش‌های غربی آلمانِ امروزی را تحت حاکمیت فرانسه قرار داد، و با رد پیمان خودش با پروسی‌ها، هانوفر را به انگلیسی‌ها پیش‌کش کرد. آنهایی که ضد ناپلئون بودند، فقط شامل پروسی‌ها و ساکسونی‌ها بودند؛ و تنها متحد آنها هم روسیه بود، که پس از شکست استرلیتز دیگر تمایلی به جنگ نداشت.

برای جلوگیری از تبدیل ساکسونی به یکی از اقمار فرانسه، پروسی‌ها آن را اشغال کردند، و برای رهبری نیروهایشان دوکِ برونزویک را فراخواندند (در آن زمان او 71 سال داشت.) ناپلئون اعلان جنگ کرد و ارتش او از سمت شمال غربی از راه ساکسونی به برلین حمله کرد. پروسی‌ها تلاش کردند نیروهای خودشان را متمرکز کنند، ولی فرانسوی‌ها نسبت به آنها بسیار سریع بودند، و واحدهای اصلی ارتش پروس را در یانا (Jena) متلاشی کردند. دوک همراه با یک دسته کوچک در اورشتدت (Auerstädt) اردو زده بود. یکی از گروه‌های ارتش ناپلئون از طرفین به او حمله کرده و نیروه‌های او را پراکنده کردند.

دوک که به طرز مهلکی زخمی شده بود با اعزام فرستاده‌ای از ناپلئون درخواست کرد که او را به خانه‌اش بفرستد تا در آنجا بمیرد. امپراطور (ناپلئون) دیکتاتوری بود که آنقدر خصلت جوانمردی نداشت تا به فرستاده او جواب مثبت دهد، بنابراین فقط به او خندید. دوکِ نابینا و بیچاره، که درحال مرگ بود، مجبور شد با یک گاری به قلمروهای آزادِ آنسوی رود آلب بگریزد. منشی ناپلئون، لویی دو بورین در خاطرات خودش با اندوه چنین می‌نویسد:

دوکِ برونزویک که در نبرد اورشتدت بشدت مجروح شده بود، در 29 اکتبر به آلتونا در نزدیکی هامبورگ رسید. ورود او به این شهر مثال روشنی از فراز و نشیب‌های زندگی او بود. مردم سلطانی را می‌دیدند، که به درست یا غلط، یک فرمانده نظامی بزرگ بود، و هر چند که تا همین اواخر در پایتخت خودش زندگی آرام و قدرمندی داشت، حالا زخمی و درحال مرگ بود. ورود او به آلتونا با یک تختِ حقیر انجام می‌گرفت که توسط ده مرد حمل می‌شد، بدون اینکه هیچ افسر یا خدمتکاری همراه آنها باشد، او تنها با بچه‌هایی که بدنبال آنها می‌دویدند بدرقه می‌شد. دوک تا روزهای پایانی زندگی‌اش، به غیر از همسرش هیچ کسی را ندید. او از پذیرش بقیه سرباز می‌زد و نهایتاً در 10 نوامبر درگذشت.

هنگام بازگشت، جسدش از برونزویک عبور کرد، و گفته می‌شود که گاوس از پنجره اطاقش که روبروی دروازه قصر بود، ارابه او را دید. از آن پس دوک‌نشینِ برونزویک منحل شد، و در قلمرو دست‌نشانده ناپلئون بنام وستفالیا ضمیمه شد. وارث دوک، فردریک ویلهلم، از ارث محروم گشت و مجبور شده به انگلستان فرار کند. او نیز در سال 1815، درست چند روز پیش از نبرد واترلو (Waterloo)[3]، در جنگ با ناپلئون کشته شد. شاید اگر چند روز بیشتر زنده بود، دوک‌نشین برونزویک دوباره به دست او می‌افتاد.

البته باید نکته‌ای را هم در رابطه با انصاف ناپلئون ذکر کنم. هنگامی که گاوس به گوتینگن رفته بود، و آلمان غربی درحال چپاول بود، با وساطت برخی از ریاضیدانان فرانسوی، که گفتند ”بزرگترین ریاضیدان جهان در آنجا زندگی می‌کند“، ناپلئون از حمله به آنجا صرف نظر کرد [4].

2.

حال که گاوس حامی خود را از دست داده بود، مجبور بود شغلی پیدا کند. در سال 1807 سرپرستی رصدخانه دانشگاه گوتینگن به او پیشنهاد شد، که وی آن را پذیرفت. بین سالهای 1798-1795، خود گاوس در آنجا مشغول تحصیل بود، و ظاهراً به کتابخانه باشکوه آنجا علاقه زیادی داشت، جایی که بیشتر عمرش را در آنجا گذراند. حالا او مدیر بخش نجوم دانشگاه شده بود و تا زمان مرگش در سال 1855، درست چند هفته پیش از 78 سالگیش، در آنجا ماند. در 27 سال آخر زندگیش، او تنها یکبار از رصدخانه محبوب‌ خودش دور ماند، آن هم زمانی بود که برای شرکت در یک کنفرانس به برلین رفته بود.

برای توضیح ارتباط گاوس با ق.ا.ا، ابتدا باید خوی عجیب او بعنوان یک ریاضیدان را توضیح دهم. گاوس اکثر نوشته‌های خودش را منتشر نمی‌کرد. بر اساس مکاتباتی که او با ریاضیدانان دیگر داشت، مقالات چاپ نشده او، و مدارک کاملی که از آثار چاپ شده او موجود است، همه حاکی از این هستند که تاکنون تنها بخشی اندکی از کارهای او کشف شده است. قضایا و اثبات‌هایی که برای دیگران مایه اعتبار بود، او تنها آنها را در یادداشت‌های روزانه شخصی خودش بصورت رمزی می‌نوشت.

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image061.png$

کارل فردریش گاوس

برای این کم‌توجهیِ ظاهری، دو دلیل بنظر می‌رسد. یکی از آنها فقدان جاه‌طلبی او بود. گاوس مردی خوددار و ساده‌زیست بود، کسی که زندگی خودش را بدون دارایی‌های مادی سپری کرده بود و بنظر می‌رسد هیچ وقت هم تمایلی به داشتن آنها نداشت. او برای کارش به کس دیگری محتاج نبود و بدنبال ترقی‌های اجتماعی هم نبود. دلیل دیگری که در میان ریاضیدانان بیشتر معمول است، کمال‌گرایی او بود. او هیچ وقت نتیجه کارهای خودش را برملا نمی‌کرد، مگر اینکه آنها بقدر کافی صیقلی، و از لحاظ منطقی بی‌عیب و نقص باشند. در مهر شخصی او نشانِ درختی با میوه‌های اندک دیده می‌شود، و در زیر آن شعار ”Pauca sed matura“ حک شده، که یعنی ”کمتر، ولی رسیده‌تر“.

هرچند گاوس هیچ حس جاه‌طلبی نداشت، ولی بی‌ملاحظه نیز بود. او در رابطه با همکارانش دردسرهای زیادی برای خودش درست کرده بود. مثلاً هنگامی که آنها کشفیاتی را مطرح می‌کردند، او ادعا می‌کرد که وی سالها قبل آنها را کشف کرده ولی آنها را منتشر نکرده. چنین چیزی از روی تکبر نبود، گاوس عاری از تکبر بود، ولی بقولی ”به طرز خشکی بی‌اعتنا“ بود. مثلاً، در کتابی که در سال 1809 منتشر شد، گاوس به روش کمترین مربعات (least squares)، که در سال 1794 کشف کرده بود، اشاره می‌کند. روش کمترین مربعات راهی برای یافتن بهترین منحنی است که در یک سری از داده‌های آماری صدق می‌کنند. البته او در آن زمان این کشف را منتشر نکرده بود. ریاضیدان پیش‌کسوت فرانسوی، آدرین-ماری لژاندر (Adrien-Marie Legendre)، این روش را در سال 1806 کشف و آن را منتشر کرد، و سپس از دست گاوس شاکی شد که چرا او ادعا می‌کند قبلاً این روش را کشف کرده. نسبت به ادعای گاوس تردیدی نیست، زیرا مدارک مستندی برای آن وجود دارد. ولی اگر او می‌خواست اعتبار این کشف را از آن خودش کند، حقیقتاً باید آن را قبلاً منتشر می‌کرد. برای گاوس اعتبار خیلی مهم نبود، و اگر برای به کمال رساندن یک موضوع وقت کافی نداشت، آن را هم منتشر نمی‌کرد.

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

فصل 5

تابع زتای ریمان

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image006.png$

15/11/1400

1.

— مسئله بازِل—

برای سری نامتناهی زیر یک فرم بسته پیدا کنید:

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image062.png$

مسئله بازِل به افتخار شهر بازل سوئیس نامگذاری شده که در آنجا برادران برنولی، یکی بعد از دیگری، استاد ریاضی بودند (یاکوب در 1705-1687 و یوهان در 1748-1705). من در بخش 3 فصل 1 به برادران برنولی اشاره کردم و گفتم آنها کسانی بودند که برای واگرا بودن سری هارمونیک اثباتی را پیدا کردند. در کتابی که یوهان منتشر کرد، اثبات خودش، و اثبات برادرش برای سری هارمونیک را ارائه داد، و سپس مسئله بازل را مطرح کرد، و گفت اگر کسی جواب آن را می‌داند، وی را مطلع کند (من بزودی معنی ”فرم بسته“ را توضیح خواهم داد).

توجه داشته باشید آن سری که مسئله بازل به آن مربوط است (که من آن را سریِ بازل می‌نامم) بی‌شباهت به سری هارمونیک نیست. در واقع تنها تفاوت آنها در این است که هر جملهِ سریِ بازل، مربع هر جملهِ سری هارمونیک است. اگر شما هر عدد کوچکتر از 1 را به توان 2 برسانید، حاصل آن عددی کوچکتر است؛ مربع یک-دوم می‌شود یک-چهارم، که از یک-دوم کوچکتر است. هر چه عدد کوچکتر باشد، مربع آن نیز کوچکتر می‌شود؛ یک چهارم کمی کوچکتر از یک-دوم است، ولی یک-صدم، که مربع یک-دهم است، خیلی از آن کوچکتر است.

بنابراین هر یک از جملات سری بازل از جملات متناطر در سری هارمونیک کوچکترند، و هر چه جلوتر می‌روید، آنها کوچکتر و کوچکتر می‌شوند. می‌دانید که سری هارمونیک به کندی واگرا می‌شد، بنابراین، انتظار زیادی نخواهد بود که جملات بازل، که به مراتب کوچکتر و کوچکتر می‌شوند، شاید همگرا شوند. محاسبات نشان می‌دهد که حقیقتاً همینطور نیز هست. مجموع 10 جمله نخست 1.5497677…، مجموع 100 جمله نخست 1.6349839…,، مجموع 1000 جمله نخست 1.6439345…,، و مجموع 10000 جمله نخست 1.6448340.… است. واقعاً بنظر می‌رسد که این سری به عددی بین 1.644 تا 1.645 همگرا شود. ولی چه عددی؟

در چنین مواقعی ریاضیدانان با بدست آوردن یک مقدار تقریبی راضی نمی‌شوند، خصوصاً وقتی سری مورد نظر، مثل سری بازل، خیلی آهسته همگرا ‌شود (مجموع 10,000 جمله تنها به اندازه 0.006 از اندازه مجموع واقعی، که 1.6449340668… است، اختلاف دارد). آیا جواب مسئله ما کسر $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image063.png$ است، یا $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image064.png$ ؟ یا شاید هم چیز پیچیده‌تری باشد که شامل جذر گرفتن باشد، مثل $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image065.png$ ، یا حتی پیچیده تر مثل $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image066.png$ ، یا $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image067.png$ ؟ جواب دقیق چیست؟ یک فرد غیر-متخصص ممکن است تصور کند که اگر جواب این مسئله چیزی (مثلِ یک کسر) باشد که اگر آن را تا ده/بیست رقم اعشار حساب کنیم و با مجموع ما سازگار بود، همان کافی است. نه، اینطور نیست! ریاضیدانان، می‌خواهند جواب دقیق آن را بدانند. دلیلش هم این نیست که آنها به طرز عجیبی وسواسی هستند، بلکه آنها بر اساس تجربه می‌دانند که بدست آوردن جواب دقیق، غالباً درهای جدید و غیرمنتظره‌ای را می‌گشاید که زیربنای مسئله را تشکیل می‌دهد. اصطلاحِ ریاضی که برای بیان دقیق اینمورد بکار می‌رود، ”فُرم بسته“ (closed form) است. گرچه یک تخمین دقیق و طولانی خوب است، ولی این یک ”فُرم باز“ است. عدد 1.6449340668… یک فرم باز است. آن سه نقطه‌ای که در انتهای عدد قرار گرفته، نشان دهنده باز بودن (بی‌انتها بودن تخمین) است.

پس مسئله بازل به اینصورت بود: برای مجموعِ معکوسِ مربعِ اعداد، یک فرم بسته پیدا کنید. این مسئله نهایتاً 64 سال پس از مطرح شدن آن، در سال 1735 با تلاش زیاد لئونارد اویلرِ جوان در سنت‌پیترزبورگ حل شد. جواب شگفت‌انگیز این مسئله $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image068.png$ است. در اینجا π همان عدد جادویی 3.1415…، یعنی نسبت محیط دایره به قطر آن است. در مسئله‌ای که اثری از دایره، یا اصلاً هندسه نیست، عدد π چه می‌کند؟ برای ریاضیدانان امروزی که عادت کرده‌اند π را در همه جا ببیند، ظهور این عدد مایه تعجب نیست، ولی برای ریاضیدانان قرن هجدهم، این موضوعِ قابل توجه‌ای بود.

مسئله بازل دری را بسوی تابعِ زتای ریمان می‌گشاید، و تابعِ زتا همان شیء ریاضی است که در قلبِ فرضیه ریمان قرار دارد. ولی پیش از اینکه ما از این در عبور کنیم، من باید چند اصل ساده ریاضی را توضیح دهم: توان‌ها، ریشه‌ها، و لگاریتم‌ها.

2.

در وهله نخست، شما زمانی با توان روبرو می‌شوید که بطور مکرر عددی را در خودش ضرب کنید. عدد 12³ یعنی 12×12×12، که سه مضروب دارد؛ 12⁵ یعنی 12×12×12×12×12، که پنج مضروب دارد. اگر من 12³ را در 12⁵ ضرب کنم چه می‌شود؟ این عبارت خواهد بود از (12×12×12) × (12×12 ×12×12×12)، که البته می‌شود 12⁸. تنها کاری که من کردم این است که توان‌ها را با هم جمع کردم، 3+5=8. این اولین قاعده مهم توان‌ها است:

x^m × xⁿ = x^{m + n} قاعده اول توان‌ها :

(اجازه دهید اشاره کنم که در تمامی این بخش منظور ما از x، مقادیر مثبت آن است. به توان رساندن 0 به هر توانی، اکثراً اتلاف وقت است، و به توان رساندن اعداد منفی مشکلات دشواری را بوجود می‌آورد که من بعداً آنها را توضیح خواهم داد.)

اگر من 12⁵ را بر 12³ تقسیم کنم چه می‌شود؟ یعنی $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image069.png$ . همانطور که می‌دانید من می‌توانم سه تا از 12ها را بالا و پایین بردارم، که نهایتاً می‌ماند $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image070.png$ ، که می‌شود 12². این ما را به قاعده دوم توان‌ها می‌رساند:

x^m ÷ xⁿ = x^{m − n} قاعده دوم توان‌ها :

فرض کنید من بخواهم 12⁵ را به توان 3 برسانم، یعنی:

(12×12×12×12×12)×(12×12×12×12×12)×(12×12×12×12×12)

که می‌شود 12¹⁵. در اینجا توان‌ها درهم ضرب می‌شوند.

(x^m)ⁿ = x^{m × n}قاعده سوم توان‌ها:

اینها اساسی‌ترین قواعد مربوط به توان‌ها هستند. من در طول این کتاب از آنها بعنوان ” قاعده اول توان‌ها“، و غیره یاد می‌کنم. من باید چند قاعده دیگر را هم در اینجا اضافه کنم، زیرا تا اینجا فقط از توان‌هایی استفاده کردم که اعداد صحیح مثبت بودند. اگر توان‌، منفی یا کسری باشند چه می‌شود؟ اگر توان صفر باشد چطور؟

از آخری شروع می‌کنم، اگر a⁰ معنی داشته باشد، باید با قواعدی که قبلاً توضیح دادم سازگار باشد. فرض کنید در قاعده دوم توان‌ها، من m را مساوی n بگیرم، بنابراین طرف سمت راست معادله حقیقتاً a⁰ خواهد بود. طرف راست نیز a^m ÷ a^m است، که a^m هرچه باشد، حاصل تقسیم 1 خواهد بود.

x⁰ = 1 : x قاعده چهارم توان‌ها برای مقادیر مثبت

از قاعده دوم توان‌ها همچنین می‌توان برای معنی دادن به توان‌های منفی نیز استفاده کرد. طبق قاعده دوم توان‌ها، حاصل تقسیم 12³ بر 12⁵، می‌شود 12⁻² . درواقع جواب عبارت است از:

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image071.png$

که اگر آن را به 12 ساده کنیم می‌شود: $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image072.png$ .

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image073.png$ ( $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image074.png$ و خصوصاً،) قاعده پنجم توان‌ها:

قاعده سوم نیز کلیدِ معنیِ توان‌های کسری است. معنی $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image075.png$ چه می‌توانم باشد؟ خوب من می‌توانم آن را به توان 3 برسانم؛ و اگر اینکار را انجام دهم، طبق قاعده سوم، حاصل آن باید x¹ باشد، که همان x است. بنابراین $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image075.png$ همان ریشه سوم x است [5]. پس قاعده سوم، معنی توان‌های کسری را به ما می‌گوید؛ $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image076.png$ یعنی ریشه سوم x به توان دو، یا بعبارت دیگر، ریشه سوم x².

x^mعدد ام nیعنی ریشه $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image077.png$ قاعده ششم توان‌ها:

بدلیل اینکه 12 مساوی 3×4 است، بنابراین، 12⁵ نیز یعنی :

(3×4)×(3×4)×(3×4)×(3×4)×(3×4)

ما می‌توانیم عبارت فوق را بصورت زیر بازنویسی کنیم:

(3×3×3×3×3)×(4×4×4×4×4)

که بطور خلاصه یعنی: 12⁵ = 3⁵ × 4⁵ . قاعده کلی بصورت زیر است:

(x × y)ⁿ = xⁿ × yⁿ قاعده هفتم توان‌ها:

درباره به توان رساندن اعداد به قوه یک عدد گنگ چه می‌توان گفت؟ مثلاً آیا $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image078.png$ ، یا $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image079.png$ ، یا $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image080.png$ معنی دارند؟ در اینجا ما به قلمرو آنالیز باز می‌گردیم. از قسمت 7 فصل 1 بخاطر دارید که دنباله‌ای که به $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image045.png$ همگرا ‌شود، این دنباله‌ است: $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image081.png$ . اگر به اندازه کافی جملات این دنباله را ادامه دهید، می‌توانید به هر اندازه که بخواهید به $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image082.png$ نزدیک شوید. به دلیل اینکه قاعده ششم معنی توان‌های کسری را به ما می‌گوید، حالا من می‌توانم تا آنجا که بخواهم مقدار توان‌های کسری 12 را حساب کنم. معلوم است که 12¹ برابر 12 است. و $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image083.png$ یعنی ریشه دوم 12 به توان سه: 41.569219381…. و $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image084.png$ یعنی ریشه پنجم 12 به توان هفت: 32.423040924. بطور مشابه $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image085.png$ می‌شود 33.794038815…، $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image086.png$ می‌شود 33.553590738، ، $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image087.png$ می‌شود 33.594688567، و غیره. همانطور که می‌بینید، این توان‌های کسری 12 به یک عدد نزدیک می‌شوند. در واقع هر چه توان‌ها به $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image082.png$ نزدیکتر می‌شوند، حاصل توان کسری نیز به عدد 33.588665890… نزدیکتر می‌شوند. پس من با اطمینان می‌توانم بگویم $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image088.png$ .

بنابراین اگر عدد مثبتِ x به توان هر عددی برسد (چه مثبت، منفی، کسری، یا گنگ) همیشه از قوانینی که ذکر کردم پیروی می‌کند، زیرا من قوانین خودم را طوری تعریف کردم که مطمئن شوم چنین قوانین پابرجا هستند! شکل 1-5 برای مقادیر مختلف a، که میان −2 تا 8 قرار دارند، نمودار x^a را نشان می‌دهد.

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image089.png$

شکل 1-5: توان‌های مختلف x.

در این نمودار خصوصاً به توان صفرم x توجه کنید، که فقط یک خط افقی است که ارتفاع آن از محور xها 1 است. این همان موردی است که ریاضیدانان به آن یک ”تابع ثابت“ می‌گویند (پرستاران بخش آی.سی‌.یو نیز به آن نمودار مسطح می‌گویند [6]). در این تابع مقدار x هرچه باشد، مقدار تابع x⁰ برابر با 1 است. همچنین توجه کنید که با افزایش مقدار صحیح a، چگونه مقدار x^a بسرعت افزایش می‌یابد (مثلاً x² , x³ , x⁸)، و توان‌های کسری، مثل x^0.5، چقدر کند افزایش می‌یابند.

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

فصل 6

هم‌آمیزی بزرگ

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image006.png$

17/11/1400

1.

لغت چینی تای‌یه (Taiye) را به ”پدرِ پدربزرگ“ ترجمه کرده‌اند. این لقبی است که خانواد همسرم به جَد پدری او داده‌ بودند [7]. هنگامی که ما در سال 2001 سفری به چین داشتیم، اولین وظیفه ما این بود که به دیدار تای‌یه برویم. خانواده همسرم خیلی به او افتخار می‌کنند، زیرا او در کمال صحت و سلامت به سن 97 سالگی رسیده بود. همه به من می‌گفتند ”حالا نود و هفت سالشه! باید حتماً اون را ببینی!“ من او را دیدم. او یک مردِ خوب و بشاش بودایی مسلک، با چهرای درخشان و گلگون بود، که هنوز ذهنی تیز و هشیار داشت. ولی نکته‌ای که برای من جالب بود این بود که آیا او واقعاً 97 سال داشت یا کمتر.

بر اساس تقویم سنتی چینی، تای‌یه در روز سوم ماه دوازدهم قمری، بنام یی‌سی، متولد شده بود. این روز بر اساس تقویم میلادی ، معادل 28 دسامبر 1905 بود. بدلیل اینکه من در اوایل ماه جولای 2001 با او ملاقات کردم، در آن زمان سن تای‌یه حدود ₂/95¹ سال می‌شد. پس چرا همه به من می‌گفتند او 97 سال دارد؟ زیرا به سبکِ چین سنتی، که تای‌یه به آن وابسته بود، او در زمان تولد یک سال داشت، و در تحویل سال جدید چینی، در حوالی 24 ژانویه 1906، درست 27 روز پس از متولد شدنش، یک سال دیگر به سن او اضافه شده بود. یعنی هنوز 1 ماه از زمان تولدش نگذشته، او 2 ساله بود! بنابراین وقتی در سال 2001 تحویل سال قمری چینی روی داد، تای‌یه آن را بعنوان شروع 97 سالگی خودش تلقی می‌کرد.

در چینِ سنتی، چیز اشتباهی در منطقِ حسابِ سن وجود ندارد. شما در یک روز بخصوص بدنیا می‌آیید این روز به یک سال بخصوص تعلق دارد. و شما آن سال بخصوص را بعنوان یکمین سال حساب می‌کنید. اگر 28 روز بعد تحویل سال نو رخ دهد، خوب، شما آن را بعنوان دومین سال تولدتان حساب می‌کنید. این کاملاً معنی می‌دهد. تنها چیزی که قضیه را عجیب جلوه می‌کند این است که در رابطه با محاسبه سن، مردمان امروزی (در چین و در کل دنیا) به این عادت کرده‌اند که زمان را به عنوان چیزی در نظر بگیرند که باید آن را اندازه گرفت. در زمان تای‌یه، چینی‌ها فکر می‌کردند که سن یک نفر چیزیست که باید آن را شمرد.

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image090.png$

خانواده نویسنده به همراه تای‌یه که از لحاظ حسابی 97 سال، و از لحاظ آنالیزی 95.522 سال سن داشت.

2.

تمایز میان اعدادی که برای شمارش از آنها استفاده می‌شود و اعدادی که برای اندازه‌گیری بکار می‌روند، بطور عمیقی در فکر و گفتار انسان رسوخ کرده است. انگار بخشی از ذهن ما جهان را بعنوان اشیاء سه‌بعدی درک می‌کند که می‌توان آنها را شمرد؛ درحالی‌که از دید بخش دیگر، ما آنها را بعنوان مجموعه‌هایی از تار و پود‌ها، ذرات، یا سیلاتی می‌بیند، که باید تقسیم شده و اندازه‌گیری شوند. چنین تمایزی سریع و آسان بدست نمی‌آید. پسر شش ساله من، هنوز لغات ”many“ و ”much“ را با هم اشتباه می‌گیرد، و مثلاً بعد از تعطیلات کریسمس از دوستش پرسید ”How much presents did you get?“[8]

درک ما از جهان در زبان‌ ما انعکاس می‌یابد. در زبان انگلیسی، جهان بطور عمده بعنوان یک جای قابلِ شمارش انگاشته می‌شود: یک گاو، دو ماهی، سه کوه، چهار در، پنج ستاره، و ... در مواردی که کمتر متداول است، زبان ما دنیا را بعنوان چیزهای قابل اندازه‌گیری می‌انگارد: دو ورقه کاغذ، دو راس گاو، دو حبه برنج، پنج گالن بنزین. هرچند لغات ”ورقه“ ، ”راس“، ”حبه“، و ”گالن“ معنی خودشان را دارند، ولی در اینجا بعنوان واحدهای اندازه‌گیری از آنها استفاده شده. برخلاف انگلیسی، زبان چینی تقریباً همه چیزها را قابل‌اندازه‌گیری می‌داند. یکی از دشواری‌های یادگیری زبان چینی حفظ کردن صحیحِ ”لغت اندازه‌گیری“ برای هر اسم است. مثلاً باید بگویید: یک راس گاو، دو چوب ماهی، سه ستون کوه، چهار بادبزن در، چهار حبه ستاره. در کُل زبان چینی، فقط دو لغت هستند که همیشه می‌توان آنها را از لحاظ دستوری بدون ذکر یک لغت اندازه‌گیری بکار گرفت: یکی از آنها ”روز“ و دیگری ”سال“ است. بقیه چیزها، گاوها، ماهی‌ها، کوه‌ها، درها، ستاره‌ها، همه جزء چیزهایی هستند که پیش از اینکه درباره آنها صحبت کنیم، ابتدا باید بخش شده و سپس اندازه‌گیری شوند.

3.

فرضیه ریمان

کلیه صفرهای غیر-ساده تابع زتا دارای بخشِ حقیقی یک-دوم هستند.

فرضیه ریمان از میان یک تقابل زاده شد، تقابل میان منطقِ شمارشی، و منطق اندازه‌گیری، همان چیزی که من در عنوان این فصل نامِ ”هم‌آمیزی بزرگ“ را به آن داده‌ام. اگر دقیقاً بخواهم این را بصورت جملات ریاضی بیان کنم، این هم‌آمیزی هنگامی روی می‌دهد که برخی از ایده‌هایی که از حساب (arithmetic) می‌آیند با برخی دیگر که از آنالیز می‌آیند ترکیب شده و چیز جدیدی را شکل می‌دهند، شاخه جدیدی از ریاضیات که نظریه تحلیلی اعداد (analytic number theory) نامیده می‌شود.

حوزه‌های سنتی ریاضیات که در بخش 8 فصل 1 نام بردم، را دوباره بصورت خلاصه نام می‌برم:

· حساب: مطالعه اعداد صحیح و کسرها.

· هندسه: مطالعه اَشکال در فضا.

· جبر: استفاده از نمادهای مجرد برای نمایش اشیاء ریاضی (اعداد، خطوط، ماتریس‌ها، تبدیلات، ...)، و مطالعه قواعد ترکیب این نمادها.

· آنالیز: مطالعه حدود.

این طبقه‌بندی چهارگانه چیزی بود که در حول و حوش سال‌های 1800 در میان ریاضیدانان پذیرفته شده بود، و هم‌آمیزی بزرگی که من قصد دارم در این فصل به آن بپردازم، هم‌آمیزی ایده‌هایی بود که تا پیش از سال 1837 بصورت مجزا، تحت عنوان یکی از این حوزه‌های اصلی، یعنی حساب و آنالیز، طبقه بندی می‌شدند. از اتحاد این دو حوزه، شاخه جدید نظریه تحلیلی اعداد بوجود آمد.

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

فصل 7

کلید طلایی، و یک قضیه اعداد اولِ بهبود یافته

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image006.png$

20/11/1400

1.

خواننده شکیبا توجه دارد که فصول ریاضی این کتاب بصورت یک در میان جلو می‌روند. فصل‌های 1 و 5 درباره مجموع‌های نامتناهی بود که نهایتاً به یک شیء ریاضی بنام تابع زتای ریمان منتهی شد؛ فصل 3 درباره اعداد اول بود، و عنوانِ آن از مقاله 1859 ریمان گرفته شده بود. در آن فصول ما قضیه اعداد اول، یا (ق.ا.ا) را توضیح دادیم. از لحاظ جذابیتی که هر دو این موضوعات (یعنی تابع زتا و اعداد اول) برای ریمان داشتند، آنها به یکدیگر مربوط نیز بودند. در واقع اگر به طریق خاصی این دو مفهوم را به هم متصل کنیم (توسط کلید طلایی)، ریمان کلِ حوزه نظریه تحلیلی اعداد را گشود. ولی او چگونه اینکار را کرد؟ این ارتباط چیست؟ کلید طلایی چیست؟ در این فصل من قصد دارم کلید طلایی را به شما نشان دهم. سپس با ارائه یک نسخه از ق.ا.ا بهبود یافته، شما را آماده کنم تا این کلید طلایی را بچرخانیم.

2.

شروع این داستان با ”غربال اراتستن“ (Sieve of Eratosthenes) بود. در واقع کلید طلایی چیزی نبود جز یک روش. همان روشی که لئونارد اویلر از آن برای بیان غربال اراتستن به زبان آنالیز استفاده می‌کرد.

اراتستن در سیرین (که امروزه شهر کوچکی در لیبی است) متولد شد. او یکی از کتابداران کتابخانه بزرگ اسکندریه بود. در حدود سال‌های 230 ق.م، تقریباً 70 سال بعد از اقلیدس، او غربال معروفش برای یافتن اعداد اول را معرفی کرد. طرز کار این غربال به این صورت بود که ابتدا کلیه اعداد صحیح از 2 به بعد نوشته می‌شوند. البته امکان ندارد که شما بتوانید همه این اعداد را بنویسید، بنابراین، مثلاً کار را با 100تا از آنها شروع می‌کنیم:

2	3	4	5	6	7	8	9	10	11	12	13	14	15
16	17	18	19	20	21	22	23	24	25	26	27	28	29
30	31	32	33	34	35	36	37	38	39	40	41	42	43
44	45	46	47	48	49	50	51	52	53	54	55	56	57
58	59	60	61	62	63	64	65	66	67	68	69	70	71
72	73	74	75	76	77	78	79	80	81	82	83	84	85
86	87	88	89	90	91	92	93	94	95	96	97	98	99

100 101 102 103 104 104 106 107 108 109 110 111 112 113

حالا از 2 شروع می‌کنیم و بدون اینکه کاری به 2 داشته باشیم، دوتا دوتا جلو رفته و به هر عددی که رسیدیم آن را حذف می‌کنیم. نتیجه چنین خواهد بود:

2	3	.	5	.	7	.	9	.	11	.	13	.	15
.	17	.	19	.	21	.	23	.	25	.	27	.	29
.	31	.	33	.	35	.	37	.	39	.	41	.	43
.	45	.	47	.	49	.	51	.	53	.	55	.	57
.	59	.	61	.	63	.	65	.	67	.	69	.	71
.	73	.	75	.	77	.	79	.	81	.	83	.	85
.	87	.	89	.	91	.	93	.	95	.	97	.	99
.	101	.	103	.	104	.	107	.	109	.	111	.	113

بعد از 2، اولین عددی که دست نخورده باقی مانده 3 است. 3 را رها کرده، ولی سه‌تا سه‌تا جلو رفته و به هر عددی که می‌رسیم آن را حذف می‌کنیم. نتیجه چنین خواهد بود:

2	3	.	5	.	7	.	.	.	11	.	13	.	.
.	17	.	19	.	.	.	23	.	25	.	.	.	29
.	31	.	.	.	35	.	37	.	.	.	41	.	43
.	.	.	47	.	49	.	.	.	53	.	55	.	.
.	59	.	61	.	.	.	65	.	67	.	.	.	71
.	73	.	.	.	77	.	79	.	.	.	83	.	85
.	.	.	89	.	91	.	.	.	95	.	97	.	.
.	101	.	103	.	.	.	107	.	109	.	.	.	113

بعد از 3، اولین عددی که دست نخورده باقی مانده 5 است. 5 را رها کرده، ولی پنج‌تا پنج‌تا جلو رفته و به هر عددی که می‌رسیم آن را حذف می‌کنیم. نتیجه چنین خواهد بود:

2	3	.	5	.	7	.	.	.	11	.	13	.	.
.	17	.	19	.	.	.	23	.	.	.	.	.	29
.	31	.	.	.	.	.	37	.	.	.	41	.	43
.	.	.	47	.	49	.	.	.	53	.	.	.	.
.	59	.	61	.	.	.	.	.	67	.	.	.	71
.	73	.	.	.	77	.	79	.	.	.	83	.	.
.	.	.	89	.	91	.	.	.	.	.	97	.	.
.	101	.	103	.	.	.	107	.	109	.	.	.	113

بعد از 5، اولین عددی که دست نخورده باقی مانده 7 است. 7 را رها کرده، ولی هفت‌تا هفت‌تا جلو رفته و به هر عددی که می‌رسیم آن را حذف می‌کنیم. پس از آن، اولین عددی که می‌ماند 11 است، و به همین ترتیب ...

اگر شما این روند را مدام تکرار کنید، اعدادی که باقی می‌مانند همه اول هستند. این غربال اراتستن است. اگر شما کارتان را پیش از رسیدن به عدد اولِ p متوقف کنید (یعنی درست پیش از اینکه pامین عددی را حذف کنید که قبلاً برداشته نشده‌اند) شما کلیه اعداد اولی را خواهید داشت که از p² کوچکتراند. در فهرست فوق، بدلیل اینکه من کارم را پیش از پردازش 7 متوقف کردم، کلیه اعداد اولی که از 7² (یعنی 49) کوچکتر هستند را دارم. پس از آن شما اعدادی مثل 77 را می‌بینید که اول نیستند.

3.

غربال اراتستن بسیار آسان است، و 2250 سال قدمت دارد. این غربال چطور در میانه قرن نوزدهم به ما رسید، و نتایجی عمیقی در نظریه توابع بجا گذاشت؟ چگونگی آن را در زیر توضیح می‌دهم.

دراینجا من قصد دارم روندی که قبلاً طی کردم را دوباره تکرار کنم. ولی اینبار می‌خواهم آن را روی تابع زتای ریمان، که آن را در انتهای فصل 5 تعریف کردم، اعمال کنم. در زیر تابع زتا را برای عددی مانند s که بزرگتر از 1 است می‌بینید:

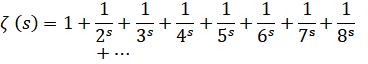
$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image091.png$

نوشتن این تابع به این روش، شامل نوشتن کلیه جملاتی است که اعداد صحیح مثبت در آن هستند، و ما هم غربال اراتستن را همینطور شروع کردیم، (البته به غیر از شامل کردن 1).

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

فصل 8

تلاشهای نه چندان بی‌ارزش

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image006.png$

25/11/1400

1.

تا اینجا مقدمات لازم برای درک فرضیه ریمان را ارائه کردم، یعنی ق.ا.ا و اشاره به مقاله 1859 ریمان و ارتباط آن با ق.ا.ا. در این فصل می‌خواهم زمینه‌های لازم برای درک مقاله ریمان را توضیح دهم. در واقع این شامل دو داستان است درهم تنیده است: یکی داستان خود ریمان، و دیگری داستان دانشگاه گوتینگن در دهه 1850، و همچنین گشتی در روسیه و نیوجرسی.

شما باید وضعیت فکری اروپا در دهه‌های 1830، 1840، و 1850 را درنظر داشته باشید. البته آن دوران با تغییرات فراوانی همراه بود. تغییراتی که بواسطه جنگ‌های ناپلئونی بوقوع پیوست، باعث برخواستن نیروهای ملی‌گرا و ترقی‌خواه شد. انقلاب صنعتی در راه بود. تغییراتی که در افکار و احساسات مردم بوجود آمده بود، و ما آنها را تحت عنوان ”جنبش رمانتیک“ می‌شناسیم، در همه‌جا و در میان اکثر طبقات رواج یافته بودند. اروپای دهه 1830 هنوز دورانِ بی‌نظمی بود، زیرا تازه شعله جنگ‌های ناپلئونی خاموش شده بود، و وقایعی مثل انقلاب ماهِ جولای فرانسه، و خیزش ملی‌گرایان لهستان (که در آن زمان بخشی از امپراتوری روسیه بود)، در میان آلمان‌ها سراسیمگی برای اتحاد ملی، و برای انگلیسی‌ها اصلاحاتِ انتخاباتی را به همراه داشت.

در آن زمان گوتینگن دوران شکوهش را پشت سر گذاشته بود، و تنها بواسطه حضور گاوس اعتبار داشت. در سال 1836 هنگامی که هفت نفر از استادان گوتینگن اخراج شدند، همانطور که قبلاً اشاره کردم، محیط گوتینگن سیاسی شد، و تاثیر اصلی آن پایین آمدن اعتبار این دانشگاه بود. پاریس مرکز تحقیقات ریاضی باقی ماند، ولی برلین نیز سریعاً درحال صعود بود. در پاریس، کوشی و فوریه با اصلاحاتی که در آنالیز بعمل آوردند، پایه‌های مدرن حد، پیوستگی، و حسابان را بنیان نهادند. پیشرفت‌های جدید در برلین با کارهای دریکله در حساب، ژاکوبی (Jacobi) در جبر، استاینر (Steiner) در هندسه، و آیزنشتاین (Eisenstein) در آنالیز آغاز شد. هر کسی که در دهه 1840 می‌خواست یک تحقیق جدی ریاضی انجام دهد، یا باید به پاریس می‌رفت یا به برلین. به همین دلیل بود که برنهارت ریمان جوان، که از استانداردهای آموزشی گوتینگن ناامید شده بود، در بهار 1847 برای تحصیل ریاضیات به برلین رفت. او در آنجا 2 سال ماند و بیش از همه تحت تاثیر لوژون دریکله قرار گرفت، یعنی همان کسی که در سال 1837 کلید طلایی را برداشته بود. دریکله به این جوان کم‌رو و تنگ دست، نوعی علاقه شخصی داشت، چیزی که بنا به گفته هاینریش وبر، ریمان آن را اینطور پاسخ می‌گفت ”من نسبت به ایشان احترام و قدردانی متقابلی را حس می‌کنم“.

ریمان پس از بازگشت به گوتینگن در 1849، تحقیق روی دکترای خودش را زیر نظر شخصِ گاوس آغاز کرد. او بسادگی انتظار داشت که مدرس دانشگاه شود، ولی این راهی طولانی بود. به منظور اینکه کسی در گوتینگن مدرس شود، نه تنها ‌باید مدرک دکترا می‌داشت، بلکه پیش‌نیاز دیگری هم برای آن بود که ”habilitation“، یا فوق‌دکترا نامیده می‌شد. برای این فوق‌دکترا نیز لازم بود رساله‌ای ارائه شود که با یک سخنرانی همراه بود. کل اینها، یعنی دکترا و فوق‌دکترا، بیشتر از پنج سال وقت ریمان را گرفت، یعنی از 22.5 سالگی تا 28 سالگی، در دورانی که او هیچ درآمدی نداشت.

ریمان همراه با درس‌های ریاضی، در چند کلاس فیزیک و فلسفه نیز ثبت‌نام کرد. در آن زمان اگر کسی می‌خواست در دبیرستان درس بدهد، و ریمان هم بدلیل اینکه نمی‌توانست در دانشگاه شغلی را بگیرد، انتخابی جز این نداشت، لازم بود دوره این رشته‌ها را گذارانده باشد. ممکن است ریمان برای احتیاط این دوره‌ها را گذرانده باشد. ولی چیزی که مشهود است این بود که او به هر دو این رشته‌ها علاقه عمیقی داشت، بنابراین امکان دارد ثبت‌نام در این دوره‌ها صرفاً بدلیل علاقه شخصی بوده باشد. استانداردها در گوتینگن نیز در حال پیشرفت بود. ویلهلم وبر فیزیکدان، که یکی از هفت نفری بود که در 1837 از دانشگاه اخراج شدند، برای تدریس به دانشگاه بازگشته بود، و حال و هوای سیاسی آنجا بطور قابل‌ملاحظه‌ای باز شده بود. وبِر (Weber) یکی از دوستان قدیمی گاوس (که با او مشترکاً دستگاه تلگراف برقی را اختراع کردند) در گوتینگن فیزیک تجربی درس می‌داد، و ریمان هم در درس‌های او شرکت می‌کرد.

2.

پنج سال کارِ تحقیقاتی بدون مواجب باید برای ریمان سخت بوده باشد. او از خانه خیلی دور بود؛ از کویک‌بورن تا گوتینگن حدود 200 کیلومتر راه بود، سفری دو روزه و ناراحت‌کننده که پرخرج نیز بود. ولی او یک همراه داشت. در 1850 ریچارد ددکیند به دانشگاه گوتینگن آمد. در آن زمان ددکیند 19 ساله بود، یعنی پنج سال جوانتر از ریمان، و می‌خواست دوره دکترای خودش را بگذراند. از نکاتی که ددکیند در مجموعه آثار ریمان نوشته اینطور بر‌می‌آید که او مهر و علاقه خاصی برای همکار بزرگترش قایل بوده، و توانایی‌های ریاضی او را ستایش می‌کرد؛ به دلیل کمبود منابع، مشکل می‌توان نظر متقابل ریمان را نسبت به ددکیند فهمید.

این دو ریاضیدان دکترای خودشان را به فاصله چند ماه از یکدیگر اخذ کردند، ریمان در دسامبر 1851، و ددکیند هم در بهار سال بعد. در آن زمان گاوس در میانه دهه 70 عمرش بود، ولی همیشه گوشش نسبت به استعدادهای استثنایی ریاضی تیز بود، و به همین دلیل رساله هر دو آنها را بررسی کرد. نظر گاوس درباره رساله ددکیند، که هنوز از لحاظ ریاضی پخته نشده بود، با نوعی تایید متداول همراه بود. ولی در مورد رساله ریمان او دست به مبالغه زد (کاری که گاوس بندرت انجام می‌داد) و گفت ”کاری ارزشمند و قابل‌توجه، که نه فقط استانداردهای لازم برای یک رساله دکترا را برآورده می‌کند، بلکه فراتر از آنها می‌رود.“

گاوس اشتباه نمی‌کرد (اصلاً من شک دارم که هیچ وقت درباره ریاضیات اشتباه کرده باشد). رساله دکترای ریمان یک اثر راه‌گشا در تاریخ نظریه توابع مختلط است. من بعداً در فصل 13 تلاش خواهم کرد نظریه توابع مختلط را توضیح دهم. ولی فعلاً کافیست که بگویم این شاخه‌‌ای قدرتمند، زیبا، و بسیار عمیق از آنالیز است. تا به امروز هم تقریباً اولین چیزی که شما در یک دوره از نظریه توابع مختلط یاد می‌گیرید معادلات کوشی-ریمان هستند که خوش-رفتاری و ارزنده بودن یک تابع را نشان می‌دهند. این معادلات به شکل مدرن خودشان ابتدا در رساله دکترای ریمان ظاهر شدند. این مقاله همچنین حاوی اولین اَشکال نظریه سطوح ریمانی هستند، یعنی پیوند نظریه توابع با توپولوژی. در آن زمان توپولوژی بقدری جدید بود که به غیر از نتایج پراکنده‌ای که در زمان اویلر حاصل شده‌ بود، به واقع هیچ دانش منسجمی درباره آن وجود نداشت. خلاصه کلام اینکه رساله دکترای ریمان حقیقتاً یک شاهکار بود.

بعد از آن، هم ریمان و هم ددکیند، برای مرحله بعدی حرفه خودشان قدم برداشتند، که آماده‌سازی رساله فوق‌دکترا، و سخنرانی بود که برای گرفتن یک منسب دانشگاهی لازم بود.

3.

اجازه دهید برنهارت ریمان را برای مدتی در اطاق خودش در گوتینگن درحالی که روی رساله فوق‌دکترای خودش کار می‌کرد رها کنیم، و در زمان 2 سال به عقب، و در مکان نیز دو هزار کیلومتر آن‌ طرف‌تر به سنت‌پیترزبورگ، بازگردیم. ما سنت‌پیترزبورگ را در زمانی رها کردیم که اویلر تحت حکم‌رانی کاترین کبیر به خوشی در آنجا زندگی می‌کرد و حتی در زمانی که پیر و نابینا شده بود بسیار پربار بود. اویلر در سال 1783، و خود کاترین هم در سال 1796 فوت شدند. جانشین کاترین، پسر وظیفه نشناس و غیرعادی او پُل بود. چهار سال سلطنت پل به نُجبا ثابت کرد که او فرد مناسبی برای حکومت نیست. به همین دلیل هم بود که او طی یک کودتا برکنار، و پسرش الکساندر به جای او بر تخت نشست. پس از آن روسیه درگیر منازعه با ناپلئون، و طبقه اشراف شد، اشرافی که همه به زبان فرانسه صحبت می‌کردند، درست شبیه همان وضعیتی که در رمان معروف تولستوی، بنام جنگ و صلح، بخوبی به تصویر کشیده شده. پس از جنگ در 1825، سلطنت به نیکولای یکم رسید، که به مراتب خودکامه‌تر بود.

ولی این خودکامگی و خودکامگی‌های مستبدان روسیه مانع از تغییرات اجتماعی نشد، و بویژه تحت تاثیر کسانی مثل، پوشکین، لرمونتوف، و گوگول تاثیرات عمیقی بر روی ادبیات مدرن روسیه گذاشت. دانشگاه سنت‌پیترزبورگ، که حالا نهاد مستقلی از آکادمی بحساب می‌آمد، رشد کرده و برومند شده بود، و دانشگاه‌های جدیدی در مسکو، خارکوف، و کازان تاسیس شده بودند. دانشگاه کازان با حضور ریاضیدان بزرگی مثل نیکلای لباچوفسکی (Nikolai Lobachevsky) بر خود می‌بالید. لباچفسکی یکی از مخترعين هندسه نااقلیدسی بود، که من بعداً در مورد آن مطالب بیشتری را خواهم گفت.

و حالا در سال 1849-1850، پس از گذشت 25 سال از حکومت نیکلای اول، زندگی روشنفکری روسیه دچار سرکوب دیگری شد، که نتیجه واکنش نیکلای به انقلابات سال 1848 اروپا بود. ثبت‌نام در دانشگاه‌ها بسیار کاهش یافت و فرمان داده شد تا دانشجویان روسی که در خارج از کشور به تحصیل مشغول بودند به کشور بازگردند. این توصیف محیطی بود که در آن یک مدرس دانشگاه سنت‌پیترزبورگ دو مقاله مهم درباره قضیه اعداد اول منتشر کرد.

این شخص پافنوتی لووویچ چِبیشف (Pafnuty Lvovich Chebyshev) بود. باید اعتراف کنم که نوشتن صحیح نام چِبیشف به حروف لاتین واقعاً یک کابوس است. هنگامی که مشغول تحقیق برای این کتاب بودم، برای نام خانوادگی این ریاضیدان به 32 املاء مختلف برخوردم، از جمله: Cebysev، Cebyshev، Chebichev،Chebycheff ،Chebychev ، و غیره و غیره.

Description: Description: Description: Title: پافنوتی لووویچ چِبیشف (1894-1821)

پافنوتی لووویچ چِبیشف (Pafnuty Lvovich Chebyshev) 1894-1821.

و اگر نام او (پافنوتی) هم از نظر شما غیرعادی بنظر می‌رسد، از این نظر شما تنها نیستید. در حوالی سال 1971، نام کوچک چبیشف نظر ریاضیدان آمریکایی فیلیپ جی. دیویس را به خودش جلب کرد. دیویس تلاش کرد تا منشا نام ”پافنوتی“ را پیدا کند، و در سال 1983 یک کتاب بامزه به نام نخ (The Thread) منتشر کرد. او در مقدمه این کتاب توضیح می‌دهد که لغتِ پافنوتی ریشه در زبان قبطی دارد (پافنوتی=”مرد خدا“)، و از مصریان مسیحی (قبطی‌ها) به اروپا آمده، و نام یکی از کشیشان کلیسای قرن چهارم میلادی بوده.

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

فصل 9

گسترش دامنه

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image006.png$

01/12/1400

1.

حالا ما به درک فرضیه ریمان نزدیک شده‌ایم. اجازه دهید بار دیگر تعریف فرضیه ریمان را یادآور شوم،

فرضیه ریمان:

بخش حقیقی کلیه صفر‌های غیر-ساده تابع زتا، یک دوم است.

ما باید ابتدا تعریف تابع زتا را بصورت ریاضی بیان کنیم. اگر s عددی بزرگتر از 1 باشد، تابع زتا بصورت زیر تعریف می‌شود:

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image091.png$

عبارت 1-9: تعریف تابع زتا

یا اگر بخواهیم بصورت پیشرفته‌تری آن را تعریف کنیم:

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image093.png$

که جملات این مجموع نامتناهی روی کلیه اعداد صحیح مثبت انجام می‌گیرد. همانطور که توضیح دادم، با اعمال روندی شبیه به قربال اراتستن روی عبارت بالا، ما عبارت زیر را خواهیم داشت:

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image094.png$

یا به عبارت دیگر

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image095.png$

که جملات ضرب نامتناهی فوق روی کلیه اعداد اول انجام می‌گیرد، بنابراین:

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image096.png$

که من این فرمول را بعنوان کلید طلایی نامگذاری کردم.

تا اینجا همه چیز خوب است، ولی منظور از ”صفر‌های غیر-ساده“ چیست؟ صفر‌های یک تابع چیستند؟ صفر‌های تابع زتا چیست؟ و چه موقع غیر-ساده می‌شوند؟

2.

فعلاً تابع زتا را به کناری می‌گذاریم. در زیر مجموع نامتناهی دیگری را می‌بینید:

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image097.png$

آیا عبارت فوق هیچوقت همگرا می‌شود؟ اگر $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image098.png$ باشد، این مجموع همان عبارت 1-1 خواهد بود که در قسمت 4 فصل 1 آن را دیدید، زیرا $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image099.png$ و $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image100.png$ ، و غیره. بنابراین $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image101.png$ ، زیرا این مقداری است که تابع به آن همگرا می‌شود. علاوه براین، اگر شما قاعده علامت‌ها را در نظر داشته باشید، آنگاه $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image102.png$ و $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image103.png$ ، و غیره. بنابراین طبق عبارت 2-1 از قسمت 5 فصل 1، $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image104.png$ . بطور مشابه، عبارت 3-1 یعنی $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image105.png$ ، درحالیکه عبارت 4- 1 $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image106.png$ را به ما می‌دهد. یک مقدار ساده دیگر برای این تابع هنگامی است که x=0 باشد، بنابراین S(0)=1، زیرا صفر به هر توانی برسد، حاصل آن صفر است، و تنها 1 می‌ماند.

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

فصل 10

یک اثبات و یک نقطه عطف

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image006.png$

04/12/1400

1.

مقاله 1859 با عنوان ”در باب تعداد اعداد اول کوچکتر از یک عدد مفروض“ تنها اثر ریمان درباره نظریه اعداد بود، و یکی از معدود کارهای او بود که در آن ایده‌های هندسی به چشم نمی‌خورد.

هر چند این مقاله، بسیار مهم و خیره‌کننده بود، ولی از برخی لحاظ رضایتبخش نبود. پیش از هر چیز، این مقاله بر اساس یک فرضیه بزرگ بنا شده بود، فرضیه‌ای که ریمان آن را به حال خودش رها کرده بود (که هنوز هم در همین وضعیت است). گفته‌های واقعی او دراینباره چنین است:

البته خواننده ممکن است بخواهد یک اثبات قوی برای این داشته باشد، ولی من پس از چند تلاش بی‌حاصل، جستجو برای چنین اثباتی را کنار گذاشتم، زیرا چنین چیزی برای تحقیقات فعلی من ضروری نیست.

بدلیل اینکه فرضیه مذکور برای ایده‌ای که ریمان مشغول تحقیق روی آن بود اهمیت حیاتی نداشت، او آن فرضیه را اثبات نشده رها کرد. چنین چیزی معقول بنظر می‌رسد. ولی این یکی از نقص‌های مقاله است. در این مقاله چندین چیزِ مهم مطرح، ولی اثبات نشده رها می‌شوند، از جمله نتیجه اصلی مقاله! (من در فصل‌های بعدی این نتیجه را توضیح خواهم داد.)

برنهارت ریمان نمونه خالصِ یک ریاضیدانِ شهودگرا بود. این نیاز به توضیح دارد. یک شخصیتِ ریاضی دارای دو مؤلفه اصلی است، یکی منطقی و دیگری شهودی. هر دو اینها در همه ریاضیدانانِ خوب وجود دارد، ولی بیشتر اوقات یکی از آنها بر دیگری غلبه دارد. نمونه‌ای از ریاضیدانان‌ بشدت منطقی، آنالیزدان آلمانی کارل وایرشتراس (Karl Weierstrass) بود، که آثار مهم خودش را در دهه‌های 1860 و 1870 تولید کرد. خواندن مقالات وایرشتراس مانند تماشای یک صخره‌ نورد است. هر قدمی که برمی‌دارد با قدم‌های قبلی هماهنگ است. پوانکاره می‌گفت که هیچ یک از کتاب‌های وایرشتراس نیست که حاوی نمودار باشد. در واقع از میان کتاب‌های او فقط یکی استثنا است، و بقیه با چنان دقت منطقی جلو می‌روند که رسیدن به مرحله بعد شفاف بنظر می‌رسد و برای فهم آنها نیازی به شهود و درک هندسی نیست. او نمونه‌ای از یک ریاضیدان منطقی است.

در قطب مقابل، ریمان قرار دارد. اگر وایرشتراوس یک صخره نورد باشد که ذره‌ ذره از مسیر خودش را به طور روش‌مند طی می‌کند تا به اوج برسد، ریمان یک طناب‌باز است، که با جسارت و اطمینان، تمام راه خودش را در هوا طی می‌کند، (چیزی که از دید تماشاگر خطرناک و ناموجه بنظر می‌رسد) ولی او از وسط آسمان به مقصدش می‌رسد، و در انتهای مقصد چیزی هست که می‌تواند آن را در دست بگیرد. واضح است که ریمان یک تخیلِ بصری نیرومند داشت، همچنین ذهنش چنان سریع به نتایجِ زیبا و پربار می‌رسید، که او همیشه نمی‌توانست مکث کرده و آنها را اثبات کند.

بنابراین مقاله 1859 او را نباید صرفاً از نظر خلوص منطقی، و یا حتی برای وضوح آن، ارزشمند تلقی کرد. چیزی که صرفاً در این مقاله مهم است اصالت روش‌های بکار گرفته توسط ریمان، و وسعت و قدرت نتایجی است که او حاصل کرده، نتایجی که برای ده‌ها، یا شاید صدها، سال برای تحقیقاتِ ریاضیدانان آینده خوراک فراهم آورده.

ریاضیدان آمریکایی هارولد ادواردز (Harold Edwards) در کتاب خودش بنام تابع زتا، درباره مقاله 1859 ریمان اینطور می‌نویسد:

پس از گذشت 30 سال از انتشار مقاله ریمان، تقریباً هیچ پیشرفتی در این حوزه حاصل نشد. گویی جامعه ریاضی به زمان نیاز داشت تا ایده‌های ریمان را هضم کند. ناگهان در یک بازه 10 ساله، آدامار، فون منگولت، و دو لا والی پوسان موفق شدند هم فرمول اصلی ریمان برای π (x) و قضیه اعداد اول، و همینطور قضایای دیگر مرتبط با آنها را اثبات کنند. در تمام این اثبات‌ها، استفاده از ایده‌های ریمان بسیار حیاتی بودند.

2.

مقاله 1859 ریمان تاثیر مستقیمی بر روی تلاش‌هایی گذاشت که برای اثبات قضیه اعداد اول (ق.ا.ا) در جریان بود. اگر فرضیه ریمان درست بود، یکی از پی‌آمدهای آن ق.ا.ا بود. ولی نتایج فرضیه ریمان نسبت به ق.ا.ا خیلی گسترده‌تر است. ق.ا.ا را می‌تواند بر اساس مفروضات ضعیف‌تری نیز اثبات کرد. اهمیت مقاله ریمان برای اثبات ق.ا.ا، در ابزارهای جدیدی بود که برای اینکار فراهم آورد (یعنی درکِ عمیقِ نظریه تحلیلی اعداد، که نهایتاً راهی را برای اثبات ق.ا.ا فراهم کرد).

ق.ا.ا در سال 1896 اثبات شد. در حد فاصل زمانی که ریمان مقاله خودش را منتشر کرد و زمانی که ق.ا.ا اثبات شد، می‌توان به رویدادهای مهم زیر اشاره کرد:

· افزایش دانش عَملی درباره اعداد اول. انتشار جداول طولانی‌تر از اعداد اول، خصوصاً جدول کولیک (Kulik) که در سال 1867 به آکادمی وین ارائه شد، و حاوی کلیه عوامل اول همه اعداد تا 100,330,200 بود. ارنست مِیسل (Ernst Meissel) روش واضحی برای محاسبه π (x)، یا همان تابع شمارنده اعداد اول، پیدا کرد. او در 1871 مقدار صحیحی برای π (100,000,000) پیدا کرد. او در 1885 مقداری را برای π (1,000,000,000) حساب کرد، که اختلاف آن با اندازه واقعی تنها 56 بود (هر چند این اختلاف تا 70 سال بعد که کامپیوترهای دیجیتال آن را حساب کردند معلوم نشد).

· در 1874 فرانز مِرتِنز (Franz Mertens) با الهام از روش‌هایی که به ریمان و چبیشف تعلق داشت، نتایج قابل قبولی را برای مجموع معکوس اعداد اول اثبات کرد. این سری، که بصورت زیر است

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image107.png$

واگرا است، هرچند سرعت واگرایی آن از سری هارمونیک کمتر است. تخمین این سری ~log(log p) است.

· در 1881 جی.جی سیلوستر (J.J. Sylvester) در دانشگاه جان هاپکینز آمریکا حدودِ چبیشف را از %10 به %4 بهبود بخشید (به بخش 3 فصل 8 رجوع کنید).

· در 1884 ریاضیدان دانمارکی یورگن گرام (Jørgen Gram) مقاله‌ای را تحت عنوان ”تحقیقاتی در مورد تعداد اعداد اول کوچکتر از یک عدد مفروض“ منتشر کرد و از طرف انجمن ریاضیدانان دانمارک برنده جایزه شد. این مقاله موجب پیشرفتی نشد، ولی پایه‌ای بود برای تلاشهای بعدی گرام، که ما آنها را بخشهای بعدی بررسی خواهیم کرد.

· در 1885 ریاضیدان هلندی توماس استيلتيس ادعا کرد که اثباتی برای فرضیه ریمان پیدا کرده است. من بعداً به این اشاره خواهم کرد.

· در 1890 آکادمی علوم فرانسه اعلام کرد که برای حل مسئله ”تعیین تعداد اول کوچکتر از یک عدد مفروض“ جایزه‌ای تعین کرده. ضرب‌العجل ارسال جواب ماه ژوئن 1892 بود. ریاضیدان جوان فرانسوی ژاک آدامار (Jacques Hadamard) مقاله‌ای را در رابطه با انواع خاصی از توابع برحسب جواب‌های آنها ارائه کرد. ریمان برای بدست آوردن فرمول π(x) به این نتایج تکیه داشت؛ درست در همین مرحله است که ارتباط میان اعداد اول و جواب‌های تابع زتا نمایان می‌شود. ولی ریمان آن را اثبات نشده رها کرد بود. ایده‌های اصلی مقاله آدامار از رساله دکترای او گرفته شده بود، که در همان سال از آن دفاع کرد. او برنده جایزه آکادمی شد.

· در 1895، ریاضیدان آلمانی هانس فون منگولت (Hans von Mangoldt) نتایج اصلی مقاله ریمان، که ارتباط میان π(x) و تابع زتا را بیان می‌کرد، اثبات کرده و آن را بصورت ساده‌تری قالب‌بندی کرد. آن موقع مشخص شد که اگر قضیه خاصی بتواند اثبات شود (قضیه‌ای که از فرضیه ریمان خیلی ضعیف‌تر بود)، آنگاه با استفاده از نتایج منگولت می‌توان ق.ا.ا را اثبات کرد.

· در 1896، ژاک آدامار، که به او اشاره کردم، به همراه ریاضیدان بلژیکی شارل دو لا والی پوسان (Charles de la Vallée Poussin) بطور مستقل از یکدیگر، قضیه ضعیف‌تر را اثبات کردند، و در نتیجه ق.ا.ا اثبات شد.

گفته می‌شد هر کس بتواند ق.ا.ا را اثبات کند جاودانه می‌شود. این پیش‌گویی تا حدی به واقعیت پیوست، زیرا دو لا والی پوسان 96 سال، و آدامار نیز 98 سال عمر کردند. آنها نمی‌دانستند که با یکدیگر درحال رقابت هستند؛ و بدلیل اینکه آنها نتیجه تحقیقات خودشان را در یک سال منتشر کردند، ریاضیدانان فکر کردند اگر اعتبار این کشف را فقط به یکی از آنها بدهند، این بی‌انصافی خواهد بود. درست مانند قله اوررست که اعتبار فتح آن میان دو نفر تقسیم شد.

در واقع بنظر می‌رسد که دو لا والی پوسان نتایج خودش را زودتر به مطبوعات ارائه داده باشد. مقاله آدامار در بولتن انجمن ریاضی فرانسه منتشر شد. آدامار یادداشتی را ضمیمه مقاله خودش کرده بود که می‌گفت از نتایج دو لا والی پوسان چیزهایی را آموخته، ولی در آخر اضافه می‌کند: ”ولی من معتقدم هیچ کس نمی‌تواند انکار کند که روش‌های من از مزیت ساده بودن برخوردار هستند.“

کسی هرگز این را انکار نکرد. اثبات آدامار ساده‌تر است؛ و این واقعیت که او قبل از اینکه مقاله‌ او بیرون بیاید از نتایج کارهای دو لا والی پوسان آگاه بوده، پس فرصت این را داشته تا آنها را بررسی کند. ولی بدلیل اینکه کارهای این دو نفر کاملاً از یکدیگر مستقل بوده، و همچنین بدلیل اینکه هر دو انسان‌های شریفی بوده‌اند و در نتیجه هیچ سوء ظنی مبنی بر حقه‌بازی وجود نداشته، این اثبات‌هایِ هم‌زمان هیچگاه موجب خصومت یا جدال نشدند. من با رضایت می‌توانم بگویم که ژاک آدامار فرانسوی و شارل دو لا والی پوسان بلژیکی در سال 1896 بطور مستقل از یکدیگر ق.ا.ا را اثبات کردند.

3.

اثبات ق.ا.ا نقطه عطفِ بزرگی در داستان ما است، آنقدر بزرگ که از این نقطه به بعد من کتاب را به دو قسمت تقسیم کرده‌ام. در وحله اول، هر دو اثباتی که در 1896 ارائه شدند به نتایج فرضیه-مانند متکی بودند. اگر آدامار یا پوسان می‌توانستند صحت فرضیه را اثبات کنند، صحت ق.ا.ا فوراً از آن منتج می‌شد. البته آنها نتوانستند فرضیه را اثبات کنند، زیرا برای کار خودشان نیازی به آن نداشتند. اگر ق.ا.ا یک چکش باشد، فرضیه ریمان یک پُتک است. این امکان وجود داشت که ق.ا.ا را از یک قضیه ضعیف‌تر (که هیچ اسمی ندارد و در زیر آمده) استنتاج کرد:

کلیه صفر‌های تابع زتا دارای بخش حقیقی کوچکتر از یک هستند.

اگر شما بتوانید قضیه بالا را اثبات کنید، آنگاه می‌توانید از نسخه 1895 نتایج ریمان که فون منگولت آن را بدست آورد استفاده کرده و ق.ا.ا را اثبات کنید. و این همین کاری بود که آدامار و پوسان در 1896 انجام دادند.

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image108.png$

شارل دو لا والی پوسان (Charles de la Vallée Poussin) 1962-1866، یکی از اثبات کنندگان قضیه اعداد اول.

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

فصل 11

دستگاه‌های مختلف اعداد

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image006.png$

09/12/1400

1.

در بخش 6 فصل 9 من برخی از صفرهای تابع زتا را نشان دادم:

ζ(−2) = 0, ζ(−4) = 0, ζ(−6) = 0، و غیره. این ما را بسوی یک روش قطعی برای درک فرضیه ریمان هدایت می‌کند، که جهت یادآوری، آن را در زیر تکرار می‌کنم:

فرضیه ریمان:

کلیه صفرهای غیر-ساده تابع زتا دارای جزء حقیقی $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image005.png$ هستند.

متاسفانه آن صفر‌هایِ صحیحِ منفی که به آنها اشاره کردم (−2, −4, −6، ...) همه جزء جوابهای ساده تابع زتا هستند. پس ... جواب‌های غیر-ساده کجا هستند؟ برای پاسخ به این سئوال، باید به قلمرو اعدادِ مختلط و موهومی وارد شویم.

خیلی از مردم با شنیدن این حرف مضطرب می‌شوند. آنها فکر می‌کنند اعداد موهومی ترسناک، عجیب، یا غیر ممکن هستند، و از دنیای ادبیات علمی-تخیلی به ریاضیات وارد شده‌اند. همه این حرف‌ها بی‌معنی است. اعداد مختلط (Complex numbers)، که اعداد موهومی (imaginary numbers) حالت خاصی از آنها هستند، از دیدگاه‌های بسیار عَملی به ریاضیات آمده‌اند. استفاده از آنها به ریاضیدانان کمک می‌کند تا مسائلی را حل کنند که به طریق دیگری نمی‌توان آنها را حل کرد. موهومی (=خیالی) بودن آنها نیز به اندازه انواع دیگر اعداد است. اگر بگویید اعداد صحیح واقعی هستند، شما مثلاً به چه صورت می‌توانید عددی مثل هفت را لمس کنید، و بگویید واقعی است؟

در مقام مقایسه، وضعیت اعداد گنگ (مثل $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image045.png$ یا π ) کمی اسرارآمیزتر، مرعوب‌کننده‌تر، و براستی حتی از $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image109.png$ هم ترسناک‌تر هستند. وضعیتی که اعداد گنگ برای فیلسوفانِ ریاضی ایجاد کردند، حقیقتاً از عدد موهومی $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image109.png$ هم بغرنج‌تر است (به بخش 2 فصل 12 درمورد سخنرانی هیلبرت و فرضیه پیوستار رجوع کنید). حتی در دوران جدید هم تلاش‌های زیادی برای نپذیرفتن اعداد گنگ صورت گرفته، و حتی ریاضیدانانِ برجسته‌ای نیز بوده‌اند که از چنین رویکردی طرفداری کرده‌اند، کسانی مثل کرونکر (Kronecker) در اواخر قرن نوزدهم، و یان براوئر (Jan Brouwer) و هرمن ویل (Weyl) در قرن بیستم. برای توضیحات بیشتر در اینمورد به بخش 5 همین فصل رجوع کنید.

2.

برای بدست آوردن یک دیدگاه متوازن از اعداد مختلط، حقیقتاً لازم است مانند یک ریاضیدان امروزی به اعداد فکر کنید. من قصد دارم همه اینها، از جمله اعداد مختلط، را برای شما توضیح دهم. فعلاً نگران این نباشید که این اعداد چه هستند.

خوب، یک ریاضیدان امروزی چگونه به اعداد فکر می‌کند؟ پاسخ: بصورت یک مشت حروف توخالی! حروفی مانند ℕ، $ℤ$ $،$ ℚ، ℝ، و ℂ.

شاید من کمی تند رفتم. جواب دیگری نیز برای این سئوال وجود دارد. ریاضیدانان اعداد را مانند عروسک‌های تو در توی روسی در نظر می‌گیرند.

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image110.png$

عروسک‌های تو درتوی روسی، که هر عروسک داخل عروسک دیگری قرار می‌گیرد.

· درونی‌ترین عروسک: اعداد طبیعی 1, 2, 3, 4, … هستند.

· عروسک بعدی: اعداد صحیح هستند. یعنی اعداد طبیعی همراه با صفر و اعداد صحیح منفی (مثلاً −31).

· عروسک بعدی: اعداد گویا هستند. یعنی اعداد صحیح به همراه کلیه کسرهای مثبت و منفی (مثلاً $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image111.png$ ، $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image112.png$ ، $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image113.png$ ).

· عروسک بعدی: اعداد حقیقی هستند، یعنی اعداد گویا، به همراه اعداد غیرگویا (گنگ) مثل $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image045.png$ ، π، e. یونانیان باستان کشف کردند که اعدادی وجود دارند که نه صحیح هستند و نه کسری، و آنها را غیرگویا، یا گنگ نامگذاری کردند.

· بیرونی‌ترین و بزرگترین عروسک: اعداد مختلط هستند.

در چنین ترتیبی، به چند نکته باید توجه داشت. اول اینکه هر یک از این اعداد به طریق خاصی نوشته می‌شوند:

· اعداد طبیعی بصورتی شبیه به ”257“ نوشته می‌شوند.

· اعداد صحیح معمولاً دارای علامتی مثل ”−34“ هستند.

· اعداد گویا غالباً بصورت کسری نوشته می‌شوند. به منظور نوشتن این اعداد به شکل کسر، آنها به دو گونه تقسیم می‌شوند. آنهایی که مقدار‌شان کمتر از 1 است (بدون توجه به علامت)، که کسور متعارف (proper fractions) نامیده می‌شوند، و بقیه که کسور نامتعارف (improper) نامیده می‌شود. $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image114.png$ نمونه یک کسر متعارف است. یک کسر نامتعارف می‌تواند بصورت کلی $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image115.png$ ، یا بصورت مرکب $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image116.png$ نوشته شود.

· برای نمایش اعداد حقیقیِ معروف، از یک علامتِ خاص استفاده می‌شود، مثلاً π یا e. خیلی از آنها را می‌توان ”بصورت بسته“ نمایش داد، مثلاً $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image117.png$ یا $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image118.png$ . درمورد بقیه، به منظور اینکه ایده‌ای از مقدارِ آنها بدهیم، آنها را بصورت اعداد اعشاری می‌نویسیم و در انتها سه نقطه می‌گذاریم، که نشاندهنده این است که ”این عدد اینجا تمام نمی‌شود، و اگر لازم باشد می‌توان ارقام دیگری را به سمت راست اضافه کرد“ مثل: 9.539316983…. یا می‌توانیم آن را مثلاً به پنج رقم اعشار گرد کنیم (9.53931).

· اعداد مختلط اعدادی شبیه به این 35.76+76.75i هستند، که بعداً درمورد آنها بیشتر توضیح خواهم داد.

چیز دیگری که باید به آن توجه داشت این است که ساکنان هر یک از عروسک‌های روسی می‌توانند شهروند عروسک بعدی باشند.

· اعداد طبیعی (مثل 257) جزء اعدادِ صحیح هستند، و می‌توان با گذاشتن یک علامت ’+‘ آنها را نمایش داد، مثلاً +257. وقتی عدد صحیحی را می‌بینید که پیش از آن یک علامت + گذاشته شده، شما می‌دانید که این یک ”عدد طبیعی“ است.

· اعداد صحیحی مثل −27، جزء اعداد گویا هستند، که می‌توانند بصورت کسرهایی نمایش داده شوند که مخرج آنها 1 است، مثلاً $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image119.png$ . وقتی یک عدد کسری را می‌بینید که مخرج آن 1 است، شما می‌دانید که این یک ”عدد صحیح“ است.

· اعداد گویا، مثل $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image120.png$ ، اعداد حقیقی هستند، و می‌توانند بصورت اعداد اعشاریِ بی‌پایان، مثل 0.33333333…، نمایش داده شوند. چیز جالبی که درمورد اعداد گویا وجود دارد این است که اگر شما بتوانید آنها را بصورت اعشاری نمایش دهید، همیشه ارقام بعد از ممیز تکرار می‌شوند (مگر اینکه مثلا بصورت $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image121.png$ باشند، که رقم تکراری آن 0 است که بعد از 5 می‌آید ولی نوشته نمی‌شود). ولی برای مثال اگر عدد گویای $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image122.png$ بصورت اعشاری نوشته شود، شبیه زیر خواهد بود:

2.4156088560885608856088…

که ارقام تکراری آن 60885هستند. اعداد غیرگویا (گنگ) هیچ موقع تکرار نمی‌شوند. ولی این به این معنی نیست که ارقام یک عدد گنگ نمی‌توانند دارای الگویی باشند. مثلاً عدد زیر

0.12345678910111213141516171819202…

یک الگوی واضح دارد، و من با اطمینان می‌توانم به شما بگویم رقم صدم، یا میلیونم، یا تریلیونم آن چیست (می‌خواهید شرط ببندید؟ این ارقام بترتیب 5 و 1 و 1 هستند). هنگامی که یک عدد حقیقی را می‌بینید که ارقام اعشاری آن تکرار می‌شوند، شما می‌دانید که این یک ”عدد گویا“ است.

· هر عدد حقیقی می‌تواند بصورت یک عدد مختلط نوشته شود. مثلاً عدد حقیقی $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image045.png$ می‌تواند بصورت عدد مختلط $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image123.png$ نوشته شود. بعداً دراینباره بیشتر توضیح خواهم داد.

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

فصل 12

مسئله هشتم هیلبرت

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image006.png$

12/12/1400

1.

هنگامی که داوید هیلبرت (David Hilbert) در آگوست 1900 برای ایراد سخنرانی در دومین کنگره بین‌المللی ریاضیدانان قدم به تالار گذاشت، 38 ساله بود. هیلبرت فرزند یک قاضی در کوینسبِرگ بود. او زمانی بعنوان یک ریاضیدان معروف شد که توانست مسئله گُردان در رابطه با نظریه تغییرناپذیرهای جبری را حل کند، و این به 12 سال قبل بازمی‌گشت.

مسئله گُردان به وجود طبقه خاصی از اشیاء مربوط است. هیلبرت اثبات کرد که این اشیاء وجود دارند، ولی آنها را تولید نکرد، یا حتی روشی برای ساخت آنها پیشنهاد نداد. ریاضیدانان چنین اثباتی را ”اثبات وجودی“ می‌نامند. هیلبرت برای اثبات خودش از یک روش ساده استفاده کرد: ”حداقل یک دانش‌آموز در کلاس هست، بیاید او را X بنامیم، و عبارات زیر در مورد او صدق می‌کنند: هیچ کدام از دانش‌آموزانِ دیگر کلاس، بیشتر از X مو روی سرشان ندارند. X کدام دانش‌آموز است؟ این چیزی است که با توجه به معلوماتی که داریم، هرگز نمی‌توانیم آن را مشخص کنیم؛ ولی می‌توانیم از وجود داشتن آن مطمئن باشیم.“ اثبات‌های وجودی در ریاضیات نوین خیلی متداول‌اند و موضوع بحث برانگیزی بحساب نمی‌آیند. ولی در آلمان 1888 اوضاع فرق می‌کرد. درست یک سال پیش از این، یکی از ریاضیدانانِ محترم آکادمی برلین، بنام لئوپولد کرونکر (Leopold Kronecker) نظرات خودش را در مقاله ”در باب مفهوم عدد“ اعلام کرد. این مقاله تلاشی بود در جهت پاک کردن آنچه او آنها را سطوح غیرضروری انتزاع از ریاضیات می‌دانست (یعنی هر چیزی که از نظر او نتوان آن را طی یک سری مراحلِ متناهی، از اعداد صحیح استنتاج کرد. او می‌گفت: ”خداوند اعداد صحیح را آفرید، باقی هر چه هست کار انسان است.“) خود ِگردان مخالف چنین رویکردی بود و نقل قول معروفی از او در رابطه با اثبات هیلبرت هست که می‌گوید: ”این ریاضیات نیست، بلکه الهیات است.“

ولی عموم ریاضیدانان راه حل هیلبرت را تصدیق کردند. سپس هیلبرت کارهای مهمی را در رابطه با نظریه اعداد جبری و بنیان‌های ریاضیات شروع کرد. او اثبات‌های جدید و درخشانی را برای غیر جبری بودن π و e ارائه کرد (که هر دو آنها رویهم رفته سه صفحه و نیم بودند). هنگامی که فون لیندمان در 1882 برای اولین بار غیر-جبری بودن π را اثبات کرد، کرونکر از استدلال و روش او تمجید کرد، ولی اضافه کرد که کار او بی‌ثمر بوده، زیرا اعداد غیر-جبری وجود ندارند! در 1885 هیلبرت کرسی ریاضیات دانشگاه گوتینگن را بدست آورد و تا زمان بازنشستگی خودش در 1930 آنجا بود.

از نظر ریاضیدانانِ مدرن، نام ”هیلبرت“ و ”گوتینگن“ بطور نزدیکی بهم پیوند خورده‌اند. هیلبرت و گوتینگن در سی سال اول قرن بیستم ریاضیات را تحت سلطه خود داشتند، و این صرفاً شامل ریاضیات آلمان نمی‌شد، بلکه کُل ریاضیات را دربر داشت. هنگامی که در 1913 فیزیکدان سویسی پل شرر (Paul Scherrer) به گوتینگن آمد گفت ”یک زندگی خردمندانهِ بی‌نظیر در گوتینگن در جریان است.“ تعداد نسبتاً زیادی از مهمترین ریاضیدانان و فیزیکدانان نیمه اول قرن بیستم یا در گوتینگن تحصیل کرده بودند یا شاگرد کسی بودند که در آنجا بود.

از شخصیت هیلبرت گزارش‌های متفاوتی به ما رسیده. پیش از هر چیز، او شخصیتی بسیار اجتماعی، یک رقصنده ماهر، و استادی محبوب بود. ولی از برخی جهات، تا آنجا که در آلمان تحت تسلط ویلهلم برای یک استاد دانشگاه امکان داشت، او شخص زن باره‌ای بود. رگه‌هایی از رفتار گستاخانه در او دیده می‌شد و بنظر می‌رسد از خفگی زندگی دانشگاهی، عادت‌ها، مقررات، و ممنوعیت‌های اجتماعی ناراضی بود. همسر یکی از استادانِ سالخورده، با گفتن اینکه هیلبرت را در رستورانی دیده که با دستیاران جوانتر خودش مشغول بازی بیلیارد است، سعی کرده بود او را بی‌آبرو کند. در طول جنگ جهانی اول، زمانی که به دلیل زن بودنِ امی نوتر (Emmy Noether)، دانشگاه از پذیرش او بعنوان یک مدرسِ ثابت امتناع کرده بود، هیلبرت درس‌هایی را بنامِ خودش اعلام کرد، و اجازه داد نوتر آنها را برگذار کند. بنظر می‌رسید که او ممتحن سهل‌گیری باشد که به شاگردانش ارفاق می‌کند.

هرچند نمی‌توان به این اشاره نکرد که هیلبرت مردی بود کمالگرا، که بخش بزرگی از انسان‌ها را بعنوان احمق طبقه‌بندی می‌کرد. این بویژه برای خود هیلبرت مایه بدبختی بود، زیرا تنها فرزندش فرانز، از یک مشکل ذهنی جدی رنج می‌برد. او قادر نبود چیز زیادی یاد بگیرد، یا بطور ثابت سر هیچ کاری بماند. او گاه و بیگاه دچار کج‌پنداری (پارانویا) می‌شد، طوری که مدتی در بیمارستان روانی بستری می‌شد. در اوایلی که این واقایع پیش آمد، از هیلبرت نقل قول شده که می‌گفت ”از حالا به بعد، من فرزندی ندارم.“

ولی در هر حال، هیلبرت کسی بود که مورد احترام شاگردان و همکارانش بود. روایات زیادی در مورد او هست، که بیشتر آنها پرعاطفه هستند. من در اینجا سه تا از آنها را نقل می‌کنم. اولین روایت، که به فرضیه ریمان هم ربط دارد، از کتاب فرهنگ زندگی‌نامه‌های کنستانس رِید نقل می‌کنم:

روزی یکی از شاگردان هیلبرت مقاله‌ای را به او داد، که در آن ادعا کرده بود فرضیه ریمان را اثبات کرده است. هیلبرت مقاله را با دقت بررسی کرد و تحت تاثیر عمقِ استدلال دانشجو قرار گرفت؛ ولی خطایی را در آن پیدا کرد که حتی بدبختانه خودش هم نمی‌توانست آن را تصحیح کند. سال بعد این دانشجو فوت کرد. هیلبرت از والدینِ عزادار خواست که اگر ممکن است او در مراسم خاکسپاری او سخنرانی کند. درحالی که بستگان و آشنایان زیر باران کنار قبر دانشجو مشغول اشک ریختن بودند، هیلبرت جلو آمد، و سخنانش را اینطور شروع کرد ”چه غم بزرگی است که چنین جوان بااستعدادی را از دست داده‌ایم، آنهم پیش از اینکه فرصت این را داشته باشد که نشان دهد چه کارهایی را می‌توانست انجام دهد ...“ ولی ادامه داد، ”باوجود اینکه اثبات این مرد جوان از فرضیه ریمان حاوی یک اشتباه بود، هنوز هم امکان دارد که روزی برای این مسئله مشهور اثباتی پیدا شود که با خطوطی که متوفی ذکر کرده بود موافق باشد“. و سپس درحالیکه در باران کنار قبر دانشجوی مرده ایستاده بود با اشتیاق ادامه داد ” تابعی از یک متغیر مختلط را در نظر بگیرید که ...!“

دومین روایت را از کتاب مارتین دیویس بنام کامپیوتر جهانی نقل می‌کنم:

مدتی بود که دیده می‌شد شلوار هیلبرت پاره است، چیزی که از نظر خیلی‌ها مایه خجالت بود. گوش‌زد نمودن این وضعیت خجلت‌بار به دستیار او، ریچارد کورانت (Richard Courant)، محول شد. کورانت که می‌دانست هیلبرت عاشق پیاده‌روی در روستا و صحبت درباره ریاضیات است، او را به پیاده‌روی دعوت کرد. او مخصوصاً جایی را برای اینکار انتخاب کرد که پر از بوته‌های خاردار بود. در همان موقع بود که کورات به هیلبرت یادآور شد که ظاهراً خاری به شلوار او گرفته و آن را پاره کرده. هیلبرت جواب داد ”اوه! نه، چند هفته‌ای می‌شود که پاره است، ولی کسی متوجه نشده!“

سومین روایت مشکوک است، ولی احتمالِ درست بودن آن زیاد است:

چند وقتی بود که یکی از شاگردان هیلبرت سر کلاس حاضر نمی‌شد. هیلبرت سراغ او را گرفت، که در به در پاسخ به او گفته شد او دانشگاه را ترک کرده تا شاعر شود. هیلبرت هم گفته بود ”از این بابت تعجب نمی‌کنم. هیچ وقت فکر نمی‌کردم او آنقدر قوه تخیل داشته باشد که یک ریاضیدان شود.“

ضمناً، هیلبرت با وجود اینکه نامش شبیه یهودی‌ها بود، یک یهودی نبود. نام او باعث شده بود که در دوران هیتلر مورد سوء ظن قرار گیرد. اجداد پدری او عضو یک فرقه بنیادگرای پرتستان بنام Pietists بودند، که طرفدار عهدِ عتیق و نام‌های انجیلی بودند.

2.

مورخ آمریکایی کنستانس رِید، هیلبرت را در کنگره 1900 اینطور توصیف می‌کند:

مردی که آن روز صبح پشت تریبون قرار گرفت هنوز چهل سال نداشت، قدی متوسط و هیکلی سفت و چابک داشت، با یک پیشانی خیلی بلند، سری طاس، که فقط پایین آن با موهای کوتاه قرمزرنگ پوشیده شده بود. عینکی روی بینی او بود. ریشی کوتاه و سبیلی نامرتب داشت. با چشمان آبی روشن که از پشت عینک معصوم ولی استوار بنظر می‌رسیدند.

هیلبرت در تالار سخنرانی دانشگاه سوربون سخنرانی خودش را به زبان آلمانی ایراد کرد. تعداد کل شرکت کنندگان حدود 250 نفر بود، ولی محتمل نیست که همه آنها برای شنیدن سخنان هیلبرت در آنجا حاضر شده باشند.

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image124.png$

داوید هیلبرت (David Hilbert) 1943-1862

عنوان سخنرانی او ”مسائل ریاضی“ بود. سخنان او برای ریاضیدانانِ قرن بیستم بسیار آشنا بود ”چه کسی از میان ما خوشحال نخواهد بود اگر نقاب از سر رازهایی برداشته شود که در پشت آینده پنهان‌اند؟“ هیلبرت در ادامه برای جلب توجه ریاضیدانان درباره اهمیت مسائلِ مشکل سخن گفت. او سخنان خودش را با فهرست کردن 23 مسئله خاص به پایان رساند.

شاید در اینجا من باید 23 مسئله هیلبرت را برای شما توضیح دهم. ولی انجام اینکار موجب طولانی‌تر شدن این کتاب می‌شود. علاوه‌ براین، نوشته‌های قابل‌توجهی وجود دارد که این مسائل را در هر سطحی تشریح می‌کند. فقط یادآور می‌شوم که مسئله اول او، یعنی فرضیه پیوستار (Continuum Hypothesis) است که در فصل قبل به آن اشاره کردم. فرضیه پیوستار قلبِ مسئله پیچیدهِ اعداد حقیقی را تشکیل می‌دهد، همان چیزی که موجب اعتراض کرونکر بود. در اینمورد نیز نوشته‌جات بسیاری وجود دارد که شما با مراجعه به یک کتابخانه خوب، یا جستجو در اینترنت می‌توانید مطالب مورد نظر خودتان را پیدا کنید.

تنها یکی از مسائل هیلبرت بطور مستقیم به موضوع این کتاب ارتباط دارد، و آن مسئله هشتم اوست.

مسئله هشتم هیلبرت؛ مسئله اعداد اول

اخیراً پیشرفت‌های قابل‌ملاحظه‌ای در رابطه با توزیع اعداد اول توسط آدامار، دو لا والی پواسان، فون منگولد، و دیگران حاصل شده. ولی برای حل کامل مسئله‌ای که در مقاله ریمان مطرح شده بود، هنوز لازم است صحتِ گزاره فوق‌العاده مهم ریمان، که گفته بود ”صفرهای تابع ζ(s) ، صرف نظر از جواب‌های ساده که شامل اعداد صحیح منفی می‌شوند، همه دارای بخش حقیقی $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image125.png$ هستند“، باید اثبات شود. زمانی که این فرضیه با موفقیت اثبات شود، مسئله بعدی شامل آزمایش دقیق سری نامتناهی ریمان، تعداد اعداد اول کمتر از یک عدد مفروض، و خصوصاً، اینکه آیا تفاوت میان اعداد اول کمتر از x، و انتگرالِ لگاریتمِ x حقیقتا با مرتبه‌ای بی‌نهایت شود که از $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image126.png$ بزرگتر نباشد. بعداً ما باید معین کنیم که آیا تراکم گاه و بیگاه اعداد اول حقیقتاً بدلیل جملات فرمول ریمان است که به صفر‌های مختلط تابع زتا بستگی دارد.

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

فصل 13

نمودارهای آرگومانی و مقداری

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image006.png$

16/12/1400

1.

فرض کنید شما را قانع کرده باشم که اعداد مختلط توسعه‌ مستقیمی از اعداد حقیقی هستند، که از کلیه قواعد عادی حساب، به استثناء i²=−1، پیروی می‌کنند؛ و بخاطر داشته باشید کاری که یک تابع انجام می‌دهد فقط تبدیل یک محدوده از اعداد (که دامنه تابع نامیده می‌شود) به محدوده دیگر است؛ حالا، آیا دلیلی وجود دارد که ما نباید تابعی از اعداد مختلط داشته باشیم؟ خیر، هیچ دلیلی برای این وجود ندارد.

مثلاً، تابع مربع همانطور که برای اعداد حقیقی جواب می‌دهد، برای اعداد مختلط هم از قوانین ضرب پیروی کرده و جواب می‌دهد. برای مثال، مربع عدد مختلط (−4+7i)² عبارت است از 16−28i−28i+49i²، که می‌شود −33−65i. جدول 1-13 مقدار تابع مربع را برای برخی از اعداد مختلط نشان می‌دهد:

z	z²
−4 + 7i	−33 − 56i
1 + i	2i
i	−1
0.174 − 1.083i	−1.143 − 0.377i

جدول 1-13: تابع مختلط z² .

در این مرحله، ممکن است باور آن سخت باشد، ولی مطالعه ”توابعِ مختلط“ یکی از ظریف‌ترین و زیباترین شاخه‌های ریاضیاتِ عالی است. دامنه کلیه توابعی که در دبیرستان با آنها آشنا شدید بسادگی می‌تواند به کلیه اعداد مختلط (یا اکثر آن) گسترش یابد. برای مثال، جدول 2-13 مقادیر تابع نمایی e^z را برای برخی از اعداد مختلط نمایش می‌دهد:

z	e^z
−1 + 2.141593i	−0.198766 + 0.30956i
3.141593i	−1
1 + 4.141593i	−1.46869 − 2.28736i
2 + 5.141593i	3.07493 − 6.71885i
3 + 6.141593i	19.885 − 2.83447i

جدول 2-13: تابع نمایی e^z .

توجه داشته باشید که وقتی من آرگومان‌ها را بصورتِ جمع بالا می‌برم (هربار به اندازه 1+i)، مقادیر تابع مختلط نیز، مانند تابع نمایی حقیقی، بصورت ضربی بالا می‌روند (هربار به اندازه 1.46869 + 2.28736i). اگر من آرگومان‌ها را طوری انتخاب می‌کردم که هربار به اندازه 1 افزایش می‌یافتند، مقدار تابع هربار به اندازه ضرب در e افزایش می‌یافت. همچنین توجه کنید که من یکی از زیباترین روابطی که در کل ریاضیات دیده می‌شود را در این جدول آوره‌ام، و آن اتحاد زیر است:

e^πi=−1

زمانی گاوس گفته بود که اگر در اولین رویارویی با اعداد مختلط، پیش از اینکه درباره این اتحاد به شما گفته شود یا در جایی آن را بخوانید، خودتان فوراً متوجه آن نشوید، هیچ وقت ریاضیدان تراز اولی نخواهید شد.

ولی اصلاً چگونه ممکن است برای e، یا هر عدد دیگری، توان‌های مختلط تعریف کرد؟ اینکار را می‌توان توسط یک سری انجام داد. عبارت 1-13 تعریف واقعی e^z را نشان می‌دهد، که در آن z می‌تواند یک عدد حقیقی یا مختلط باشد:

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image127.png$

عبارت 1-13.

این سری نامتناهی بطور شگفت انگیزی برای کلیه اعداد همگرا می‌شود. مخرج کسرها چنان سریع رشد می‌کنند که هر توانی از اعداد که در صورتِ کسر قرار دارند را تحت‌تاثیر قرار می‌دهد. چیزی که به همان اندازه شگفت‌انگیز است، این است که اگر z یک عدد طبیعی باشد، این سری نامتناهی دقیقاً همانطور کار می‌کند که شما از مفهوم ”توان“ انتظار دارید، هرچند اگر به عبارت 1-13 نگاه کنید، هیچ دلیل روشنی دیده نمی‌شود که چرا اینطور است. اگر z=4 باشد، همان جوابی را خواهد داد که از محاسبه e×e×e×e بدست خواهید آورد، یعنی e⁴.

اجازه دهید در عبارت 1-13 بجای z عدد πi را بگذارم، تا به شما نشان دهم این عبارت همگرا می‌شود. اگر z=πi باشد، آنگاه z²=−π² می‌شود، z³=−π³i می‌شود، z⁴=π⁴ می‌شود، z⁵=π⁵i می‌شود، و غیره. با خوراندن این اعداد به سری نامتناهی 1-13، و محاسبه توان‌های واقعی π (برای سادگی، فقط به اندازه 6 رقم اعشار)، مجمع فوق بصورت زیر درمی‌آید:

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image128.png$

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image129.png$

اگر شما مجموع 10 جمله اول این سری را محاسبه کنید، عدد −1.001829104 + 0.006925270i را بدست می‌آورید؛ اگر 20 جمله اول را حساب کنید عدد −0.9999999999243491 − 0.000000000528919i را بدست خواهید آورد. کاملاً واضح است که سری فوق به سمت −1 همگرا می‌شود، زیرا بخش حقیقی به سمت −1 و بخش موهومی به سمت 0 می‌رود.

آیا تابع لگاریتی را نیز می‌توان به اعداد مختلط گسترش داد؟ البته که می‌توان. این تابع معکوس تابع نمایی است. اگر e^z=w ، آنگاه z=log w. مانند تابع ریشه دوم، متاسفانه اینجا نیز در باتلاق توابع چند-مقداری گیر خواهید افتاد، مگر اینکه احتیاط‌های لازم را انجام دهید. دلیلش هم این است که در دنیای اعداد مختلط، گاهی اوقات تابع نمایی برای آرگومان‌های متفاوت، مقادیر یکسانی را می‌دهد. مثلاً، طبق قاعده توان‌ها −1³ می‌شود −1؛ بنابراین اگر شما طرفین تساوی e^πi=−1 را به توان 3 برسانید، حاصل e^3πi=−1 خواهد بود؛ بنابراین، همانطور که تابع x² برای آرگومان‌های 2 و −2 مقدارِ یکسان 4 را خواهد داد، تابع e^z نیز برای دو آرگومان πi و 3πi مقدارِ یکسان −1 را خواهد داد. خوب پس، log (−1) چیست؟ πi است یا 3πi؟

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

فصل 14

اولین دغدغه‌ها

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image006.png$

22/12/1400

1.

البته در اوایل قرن بیستم، گوتینگن تنها جایی نبود که ریاضیدانان تراز اول در آنجا مشغول بکار بودند. در انگلستان، ریاضیدان جوانی بنام جان لیتل‌وود (John Littlewood) در ترینیتی کالج کمبریج مشغول بکار بود. لیتل‌وود در 1907 سخت در تلاش بود تا برای تحقیقات دوره ارشد خودش مسئله‌ای را حل کند. او در اینباره می‌گوید:

حالا بارنز می‌خواهد مسئله جدیدی را به من پیشنهاد دهد، و آن ”اثبات فرضیه ریمان“ بود. راستش را بخواهید، این پیشنهادِ پرخطر آنقدرها هم بی‌حاصل نبود؛ ولی پیش از آن من باید زمینه تابع ζ (s) و اعداد اول در سال 1907، و خصوصاً آنچه که به من مربوط است، را توضیح دهم. آشنایی من با تابع ζ (s) از طریق کتاب لیندلوف (Lindelöf) بود، ولی در آنجا هیچ صحبتی از اعداد اول، یا اینکه آنها کوچکترین ارتباطی با تابع زتا دارند نبود. برای من فرضیه ریمان مسئله معروفی بود، ولی فقط در حوزه توابع انتگرال؛ این کار از نظر من بسیار پیچیده،‌ و خارج از جریان‌های اصلی ریاضیات بود . مقاله معروف ریمان در مجموعه آثار او آمده، و در آنجاست که ریمان فرضیه معروف خودش در رابطه با π(x)و ق.ا.ا را مطرح می‌کند، ولی آن را بدون ‌اثبات رها کرده.

مطالب فوق را از کتاب مجموعه آثار لیتل‌وود انتخاب کردم، که حاوی بخش‌هایی از شرح‌حال خودش، جُک‌ها، معماهای ریاضی، و شخصیت پردازی‌هایی است که اولین بار در 1953 منتشر شد.

2.

پیشرفت و توسعه ریاضیات در بریتانیای قرن نوزدهم بطور عجیبی نامتقارن بود. در این قرن پیشرفت‌های فراوانی توسط ریاضیدانان انگلیسی صورت گرفت، که اکثر آنها به حوزه‌ ریاضیاتِ کاربردی تعلق داشتند تا به ریاضیاتِ محض، موضوعاتی که بیشتر با فیزیک مرتبط بودند. زمانی که دانشجو بودم متوجه یک واقعیت شدم و آن اینکه وقتی ما سر یک کلاس آنالیز حقیقی، یا توابع مختلط، یا نظریه اعداد، یا جبر می‌نشستیم، قضیه‌هایی که در این حوزه‌ها مطرح می‌شد با نام کسانی پیوند خورده بود که خارج از بریتانیا بودند: کوشی، آدامار، ژاکوبی، چبیشف، ریمان، هرمیت، باناخ، هیلبرت و ...، ولی وقتی در کلاس‌هایی شرکت می‌کردیم که به فیزیکِ ریاضی مربوط بود (یعنی روش‌های ریاضی که در فیزیک بکار گرفته می‌شوند)، ناگهان دوباره به انگلستان باز می‌گردیم: قضیه گرین (1828)، فرمول استوک (1842)، عدد رینولدز (1883)، معادلات ماکسول (1855)، کارهای هامیلتون (1834) ...

فعالیت‌های دیگری که در بریتانیا انجام گرفت به حوزه‌های بسیار انتزاعی ریاضیات تعلق داشت. مثلاً آرتور کیلی (Arthur Cayley) و جی.جی سیلوستر (J.J. Sylvester) ماتریس‌ها (که بعداً در مورد آنها توضیح می‌دهم) و نظریه ناورداهای جبری (Algebraic invariants) را اختراع کردند. جرج بول با نوشتن کتاب ”قوانین فکر“، به قلمرو کاملاً جدید ”بنیان‌ها“، یا منطقِ ریاضی، قدم گذاشت. شما می‌توانید استدلال کنید که آیا حقیقتاً منطق در آخرین سطوح انتزاع قرار دارد یا نه. خود بول اعلام کرده بود که قصدش این است که منطق را بصورت یکی از شاخه‌های ریاضیاتِ کاربردی درآورد. ولی فکر می‌کنم برای بیشتر ما، منطق ریاضی به اندازه کافی انتزاعی باشد. جالب است اشاره کنم که پیش از اینکه هیلبرت سخنرانی معروف خودش را در دانشگاه ارائه دهد، درست یک ماه قبل در آنجا ”کنگره بین‌المللی فلسفه“ برگزار شده بود. عنوان یکی از مقالاتی که در آنجا عرضه شد ”ایده ترتیب و مکانِ مطلق در فضا و زمان“ بود که توسط منطق‌دان جوان بریتانیایی برتراند راسل (Bertrand Russell) ارائه شده بود، که او نیز در ترینیتی کالج درس می‌داد. ده سال بعد، راسل به همراه آلفرد نورث وایت‌هد اثر کلاسیک منطق ریاضی (یا دقیقتر بگویم ریاضیاتِ منطق‌زده) به نام اصول ریاضیات (rincipia Mathematica) را منتشر کردند.

حوزه‌های ریاضی که کمتر انتزاعی بودند، یا در حد میانه قرار داشتند، مثل نظریه توابع، نظریه اعداد، و بیشتر جبر، در بقیه اروپا رشد کردند. در آنالیز، یعنی پربارترین حوزه ریاضیات قرن نوزدهم، خبری از بریتانیایی‌ها نبود. در پایان قرن نوزدهم، آنها حتی در حوزه‌هایی که قوی بودند نیز دیده نمی‌شدند. در کنگره بین‌المللی ریاضیدانان در پاریس تنها 7 بریتانیایی شرکت کردند، که در مقایسه با بقیه اروپا بسیار کم بود، فرانسه (90 نفر)، آلمان (25)، آمریکا (17)، ایتالیا (15)، بلژیک (13)، روسیه (9) اطریش و سوئیس (هرکدام 8 نفر). در واقع، از لحاظ ریاضی، بریتانیای سال 1900 جای عقب مانده‌ای بود.

ولی حتی در جاهای عقب مانده نیز کانون‌های فعالیت دیده می‌شود. در ترینیتی کالج کمبریج، یعنی جایی که لیتل‌وود آنجا بود، یک سنت قوی ریاضی جریان داشت. میان سال‌های 1661-1693 اینجا خانه سر ایزآک نیوتون، و چندین ریاضیدان و فیزیکدان نابغه بود، از جمله: چارلز بابج (Charles Babbage)، که عموماً بعنوان مخترع کامپیوتر شناخته می‌شود؛ جورج ایری (George Airy) ستاره‌شناسی که خانواده‌ای از توابع ریاضی به نام اوست؛ آگوستوس دو مورگان (Augustus de Morgan) منطق دان؛ آرتورکیلی متخصص جبر؛ جیمز کلارک مکسول (Arthur Cayley) فیزیکدان، و برخی دیگر. برتراند راسل در 1893 مدرک خودش را از ترینیتی گرفت، و در 1895 بعنوان یکی از اعضاء هیئت علمی برگزیده شد، و زمانی که هاردی به این دانشگاه پیوست، او مشغول تدریس بود. تاریخچه کالجِ ترینیتی در قرن بیستم کمی ناهمسان بود. این دانشگاه منبع صادرکننده بیشتر افرادی بود که بعداً به حلقه جاسوسی کمبریج معروف شدند. تا جایی که به ریاضیاتِ آغازِ قرن بیستم مربوط است، ترینیتی خانه گادفری هاردی (Godfrey Hardy) بود. بیش از هر کس دیگری، این هاردی بود که ریاضیاتِ محضِ انگلستان را از خواب عمیقی که در آن بسر می‌برد بیدار کرد.

هنگامی که هاردی در 1897 برای گرفتن دکترای خودش در ترینیتی مشغول مطالعه بود، به کتاب درس‌هایی در آنالیز (Cours d’Analyse) نوشته ریاضیدان فرانسوی کامیل ژردان (Camille Jordan) برخورد. برای دانشجویانی که نظریه توابع مختلط را مطالعه می‌کنند، نام ژردان به قضیه ژردان گره خورده، که اگر بخواهم بطور ساده بگویم می‌گوید یک منحنی بستهِ ساده در صفحه، مثل یک دایره، یک درون دارد و یک بیرون. اثبات این قضیه بسیار دشوار است، و این کاریست که ژردان انجام داد. بنظر می‌رسد که کتاب ژردان تاثیر عمیقی روی هاردی گذاشت. در همان تابستانی که هیلبرت سخنرانی خودش را در پاریس ایراد کرد، هاردی نیز به عضویت ترینیتی درآمد و چند سال مشغول انتشار مقالاتی درباره آنالیز بود.

یکی از دست‌آوردهای اولیه هاردی، که حاصل درگیری او با آنالیز بود، کتاب دوره ریاضیات محض بود که در 1908 منتشر شد و هیچ وقت چاپ‌های بعدی آن متوقف نشد. من، و بسیاری دیگر از دانشجویان دوره کارشناسی ریاضی در انگلستانِ قرن بیستم، آنالیز را از طریق این کتاب یادگرفتیم. ما کاری به عنوان کتاب نداشتیم، و از آن بعنوان ”کتابِ هاردی“ یاد می‌کردیم. عنوان این کتاب کلاً گمراه کننده است، زیرا هیچ چیز درباره آنالیز در عنوان آن دیده نمی‌شود. این یکی از کامل‌ترین کتاب‌های درسی آنالیز کلاسیک (یعنی قرن نوزدهمی) است. این کتاب روی خود من تاثیر زیادی گذاشت و رویکردم به ریاضیات را شکل داد. حالا که به نوشته‌های کتابِ خودم نگاه می‌کنم، هاردی را در آن می‌بینم.

3.

جی. اچ. هاردی شخص غریبی بود که فقط در انگلستان قرن نوزدهم می‌توانست تولید شود. او در دوران سالخوردگی خودش کتاب عجیبی بعنوان ”دفاعیات یک ریاضیدان (1940)“ نوشت، که در آن زندگی خودش بعنوان یک ریاضیدان را شرح داد. به نوعی، این کتاب غم‌انگیز است (دقیقتر بگویم، مرثیه‌گونه است). دلیل آن هم بخوبی در مقدمه‌ای که سی.پی اسنو بر چاپ‌های بعدی آن نوشته معلوم است. هاردی یک ”بِیبی فیس“ بود، پسری که هرگز پیر نمی‌شد. لیتل‌وود می‌گوید ”زندگی او تا وقتی پیر نشده بود مانند زندگی یک مرد جوانِ سرزنده بود. روحیاتش، بازی‌هایش، علائق‌اش همه مانند یک استاد جوان بود. تا وقتی هنوز 30 سالش نشده بود، بسیار جوان بنظر می‌رسید.“ بازی‌هایی که هاردی به آنها بسیار علاقه داشت یکی کریکت و دیگری court tennis بود (نوعی تنیس که سخت‌تر از تنیس معمولی است).

میان سال‌های 1931-1919، هاردی به مدت 12 سال در دانشگاه آکسفورد یک کرسی داشت، در 1929-1928 در پرینستون بود؛ و بقیه عمرش را در ترینیتی کمبریج گذراند. مردی جذاب و خوش‌‌قیافه که هرگز ازدواج نکرد، و تا آنجا که معلوم است، هیچ وابستگی عاطفی هم به کسی نداشت. باید بخاطر داشت که آکسفورد و کمبریج، موسساتی فقط-مردانه بودند که در آنجا رایحه زن-گریزی به مشام می‌رسید. تا سال 1882، استادان ترینیتی اجازه ازدواج

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image130.png$

گاتفرید هاردی (G.H. Hardy) 1947-1877

نداشتند. طبق روال امروزی، اخیراً صحبت‌هایی مطرح شده که شاید هاردی همجنس‌گرا بوده. در اینمورد من خواننده کنجکاو را به کتاب رابرت کانیگل به نام ”مردی که بی‌نهایت را می‌شناخت“ ارجاع می‌دهم. این کتاب شرح حال دوست و شاگرد هاردی سرینیواسا رامانوجان است و در آن بطور کامل به این مورد اشاره می‌کند. جواب این سئوال این است: شاید او همجنس‌گرا نبوده، اما در خصوصی‌ترین حالات، احتمال دارد که چنین بوده باشد.

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

فصل 15

نمادِ O بزرگ و تابع µ موبیوس

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image006.png$

26/12/1400

1.

من این فصل را به دو موضوع ریاضی اختصاص داده‌ام که با فرضیه ریمان ارتباط دارند، ولی با یکدیگر ارتباطی ندارند. یکی از این موضوعات نماد اوی بزرگ، ودیگری تابع µ (مو) موبیوس است. ابتدا اوی بزرگ.

2.

هنگامی که در 1976 ریاضیدان بزرگ مجارستانی پل توران (Paul Turán) بعلت ابتلا به سرطان فوت کرد، همسرش در کنار بسترش بود. از او نقل قول شده که می‌گفت آخرین چیزی که توران زیر لب زمزمه می‌کرد این بود ”اوی بزرگ یک ...“ ریاضیدانان با تعجب و تحسین این داستان را روایت می‌کنند. این نمونه‌‌ای از درگیری یک ریاضیدان واقعی با نظریه اعداد تا آخرین لحظه است.

اوی بزرگ (Big oh) از سال 1909، از طریق کتابِ راهنمای لاندو به ریاضیات وارد شد. همانطور که قبلاً اشاره کردم، این کتاب بسیار تاثیرگذار بود. درواقع این لاندو نبود که اوی بزرگ را اختراع کرد. او خالصانه در صفحه 883 کتاب اشاره می‌کند که وی این نماد را از رساله 1894 پل باخ‌‌مان (Paul Bachmann) اقتباس کرده. بنابراین، بی‌انصافی خواهد بود اگر همیشه از آن بعنوان ”اوی بزرگ لاندو“ یاد کنیم. ولی بیشتر ریاضیدانان احتمالاً تصور می‌کنند که لاندو این را اختراع کرده. ”اوی بزرگ“ در سراسر نظریه تحلیلی اعداد دیده می‌شود، و به بسیاری از حوزه‌های دیگر ریاضی هم رخنه کرده.

اوی بزرگ روشی برای حد گذاشتن روی اندازه یک تابع است که (معمولاً) آرگومان آن به سمت بی‌نهایت می‌رود.

تعریف اوی بزرگ:

اگر برای آرگومان‌هایی که به اندازه کافی بزرگ باشند، اندازه A هیچ وقت از ضریب ثابت B تجاوز نکند، تابع A یک اوی بزرگِ تابع B است.

اجازه دهید به گفته پل توران اشاره کنم و ”اوی بزرگ 1“ را شرح دهم. در اینجا ”1“ یک تابع است، یکی از ساده‌ترین تابع‌های ممکن، که نمودار آن بصورت یک خط راست افقی است، که به اندازه یک واحد از محور xها فاصله دارد. برای هر آرگومانی مثل x، مقدار این تابع همیشه برابر 1 است. بنابراین این چه معنی می‌دهد اگر بگوییم تابعی مثل f(x) ، اوی بزرگ 1 است؟ طبق تعریفی که قبلاً ارائه دادم، این یعنی همانطور که آرگومان x به سوی بی‌نهایت می‌رود، مقدار f(x) هیچ وقت از یک ضریب ثابت 1 بیشتر نمی‌شود. به عبارت دیگر، نمودار f(x) همیشه زیر یک خط افقی قرار می‌گیرد (که جای آن بستگی به ضریب دارد). این اطلاعات مفیدی را درباره f(x) به ما می‌دهد. خیلی از توابع هستند که چنین چیزی درمورد آنها صادق نیست. مثلاً، این درمورد x² صحت ندارد، یا برای هر عدد مثبت مثل x در تابع e^x، یا حتی برای log x.

درواقع، معنی اوی بزرگ کمی بیشتر از این است. توجه کنید که من در تعریف خودم گفتم ”اندازه A ...“ که یعنی ”مقدار A، بدون توجه به علامت آن“. اندازه 100 برابر 100 است؛ اندازه −100 نیز برابر 100 است؛ علامت برای اوی بزرگ اهمیتی ندارد. اینکه بگوییم تابعی مثل f(x) اوی بزرگ یک است، مثل این است که بگوییم f(x) میان دو خط افقی گیر افتاده، که یکی از آنها در بالای محور xها قرار دارد و دیگری با فاصله یکسان، زیر محور xها.

همانطور که گفتم، خیلی از توابع اوی بزرگ 1 نیستند. ساده‌ترین آنها تابع f(x)= x است (یعنی تابعی که همیشه مقدار آن با آرگومان آن مساوی است). نمودار این تابع بصورت یک خط صاف مورب است، که از گوشه سمت راست بالای کاغذ خارج می‌شود. واضح است که چنین تابعی میان هیچ دو خط افقی جا نمی‌گیرد. فرق نمی‌کند که شما میان این خطوط افقی چقدر فاصله بگذارید، تابع f(x)= x بالاخره آنها را درجایی قطع می‌کند. اگر شما با دادن یک ضریب به x، شیب خط مورب را نیز کم کنید، باز هم این مورد صادق است. مثلاً توابعی که مساوی 0.1x، 0.01x، 0.001x، و 0.0001x هستند، سرانجام همه آنها هر خط افقی ثابتی که بعنوان محدود کننده در نظر بگیرید را قطع خواهند کرد، بنابراین هیچ کدام از آنها اوی بزرگ 1 نیستند. (نمودار تابع f(x)=.01x در شکل 1-15 نشان داده شده)

این نکته دیگری را نیز درباره اوی بزرگ نشان می‌دهد. اوی بزرگ نه تنها به علامت‌ مثبت و منفی بی‌توجه است، بلکه درمورد ضریب هم چنین است. اگر A اوی بزرگ B باشد، آنگاه 10A، 100A، 10000000A، و غیره نیز یک اوی بزرگ B هستد. اوی بزرگ به شما نرخ دقیق رشد را نمی‌گوید (برای اینکار ما از مشتق‌ استفاده می‌کنیم)، بلکه گونه نرخ رشد را به شما می‌گوید. تابع f(x)=1 هیچ نرخ رشدی ندارد؛ کاملاً صاف است. تابعی که اوی بزرگ 1 باشد هیچ وقت سریعتر از آن رشد نمی‌کند. البته ممکن است کارهای دیگری را انجام دهد: مثلاً به سمت صفر برود، میان خطوط محدود کننده خودش تاابد نوسان کند، یا به یکی از این خطوط محدود کننده نزدیک و نزدیکتر شود، ولی هیچ وقت ناگهان از آنها بیرون نخواهد زد.

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image131.png$

شکل 1-15: تابع f(x)= x یک اوی بزرگ 1 نیست.

توابع 0.1x، 0.01x، 0.001x، و 0.0001x اوی بزرگ 1 نیستند، همه آنها اوی بزرگ x هستند. این درمورد هر تابع دیگری که میان خطوط ax و انعکاس آن، یعنی −ax، محدود شود نیز صدق می‌کند. شکل 2-15 مثالی را نشان می‌دهد که دراینمورد صدق نمی‌کند. این نمودار تابع مربع، یا x²، است. هر چقد هم که شما ضریب a‌ را بزرگ انتخاب کنید تا دو خط محدود کننده از هم فاصله بگیرند، بلاخره نمودار x² خط بالایی را قطع کرده و از آن عبور می‌کند.

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image132.png$

شکل 2-15: تابع 0.1x² یک O(x) نیست.

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

فصل 16

صعود از خط مرزی

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image006.png$

5/1/1401

1.

در 1930 هیلبرت 68 ساله شد. مطابق با قوانین دانشگاه گوتنبرگ، او در آن سال بازنشسته می‌شد. از آن زمان به بعد، امتیازات ویژه یکی بعد از دیگری برای او سر می‌رسید. یکی از آنها این بود که به این شهروند برجسته کلید شهر را اعطا کنند. این مراسم قرار بود در افتتاح کنفرانسی برگذار ‌شد که موعد آن پاییز بود. این کنفرانس با مشارکت جمعی از دانشمندان و فیزیکدانان برجسته آلمان برگذار می‌شد. بطور طبیعی چنین مراسمی به یک سخنرانی نیاز داشت. بنابراین در 8 سپتامبر 1930، هیلبرت دومین سخنرانی بزرگِ خودش را ارائه داد.

عنوان سخنرانی او این بود ”منطق و فهم طبیعت“. هدف هیلبرت این بود که برخی از نظراتی که درباره رابطه میان زندگی درونی ما (روندهای ذهنی ما، از جمله آنهایی که در ایجاد و اثبات حقایق ریاضی به ما کمک می‌کنند)، و جهان فیزیکی وجود دارد را بیان کند. البته این موضوعی بود که از یک سرچشمه طولانی فلسفی برخوردار بود، موضوعی که یکی دیگر از شهروندان معروف کوینسبرگ، یعنی فیلسوف بزرگ قرن هجدهم آلمان، ایمانوئول کانت (Immanuel Kant) بویژه در آن تخصص داشت. همانطور که بعداً در فصل 20 توضیح خواهم داد، اتفاقاً این موضوعی است که درک نوین فرضیه ریمان به آن مربوط است. هرچند در زمانی که هیلبرت در کوینسبرگ سخنرانی می‌کرد، چنین چیزی معلوم نبود.

پس از سخنرانی اصلی، طوری برنامه‌ریزی شده بود که نسخه کوتاه‌تری از آن نیز از طریق رادیو پخش شود، چیزی که در آن زمان جدید محسوب می‌شد. نسخه کوتاه سخنرانی روی صفحه‌های 78 دور گرامافون ضبط و پخش شد. ولی حالا می‌توان فایل صوتی آن را روی اینترنت نیز پیدا کرد. در متنِ این سخنرانی، شش کلمه هست که هیلبرت بخاطر آن معروف است، و شما با اندک تلاشی می‌توانید این شش کلمه بیاد ماندنی را با صدای خودش بشنوید. اینها همان کلماتی هستند که روی سنگ قبر او حک شده‌اند.

هیلبرت بطور محکم به قدرت درک ذهن انسان برای آشکارسازی حقایق طبیعت و ریاضیات اعتقاد داشت. هنگامی که او جوان بود، نظریات بدبینانه فیلسوف آلمانی امیل دوبوا-ریمون (Emil du Bois-Reymond) بسیار طرفدار داشت. ریمون معتقد بود که چیزهای خاصی (مثلاً، سرشت ذهن انسان) بطور ذاتی غیرقابل شناخت هستند. او می‌گفت ”ما ناآگاه هستیم، و ناآگاه هم خواهیم ماند.“ هیلبرت هیچ وقت از چنین فلسفه تاریکی خوشش نمی‌آمد. پاسخ او نسبت به این دیدگاه در آخرین سخنرانی عمومی وی طنین‌انداز بود.

ما نباید به آنهایی باور داشته باشیم که امروزه با اتخاذ رویکردهای فلسفی و لحنی آمرانه و از بالا، زوال فرهنگ را پیش بینی کرده و ناشناخته‌ها را توجیه می‌کنند. برای ما هیچ موضوعی که ناشناختنی باشد وجود ندارد، و به عقیده من در علوم طبیعی نیز وضع چنین است. به جای این نادانسته‌های ابلهانه، بگذارید، شعار ما این باشد: ”ما باید بدانیم - ما خواهیم دانست“.

آن شش کلام آخر، یعنی ”ما باید بدانیم - ما خواهیم دانست“ (که به آلمانی می‌شود Wir müssen wissen, wir werden wissen و روی سنگ قبر هیلبرت حک شده‌ است) معروف‌ترین نقل‌قول هیلبرت، و یکی از معروف‌ترین‌ها در تاریخ علم است. آنها بیانگر یک خوش‌بینی قوی هستند، آن هم از طرف مردی که به پیری و بیماری پا گذاشته بود.

2.

هنگامی که هیلبرت در 1930 بازنشسته شد، دانشگاه گوتینگن همان وضعیت 80 سال قبل خودش را داشت، مرکزی بزرگ برای مطالعات و تحقیقات ریاضی، شاید بزرگترین مرکزی که در آن زمان در جهان وجود داشت. چهار سال بعد گوتینگن به یک پوسته خالی بدل شد که بزرگترترین متفکرینِ جهان از آنجا می‌گریختند، یا مجبور به ترک آنجا می‌شدند.

البته مهمترین حوادث در ماه‌های اولیه 1933، و در زمانی اتفاق افتاد که آدولف هیتلر بعنوان صدراعظم آلمان سوگند یاد کرد. سپس پارلمان منحل، و انتخابات جدیدی برگذار شد که نازی‌ها 44 درصد از آرا به خودشان اختصاص دادند. تا ماه آوریل آن سال، نازی‌ها تقریباً کنترل کامل آلمان را بدست داشتند.

یکی از اولین احکامی که نازی‌ها در 7 آوریل 1933 صادر کردند اخراج کلیه یهودی‌هایی بود که در سمت‌های دولتی مشغول بکار بودند. البته بهتر است بگویم ”قصد آنها این بود“، زیرا فیلد مارشال سالخورده، پُل فون هیندنبرگ، هنوز رئیس جمهور آلمان بود و نازی‌ها برای به انجام رساندن اهداف خودشان باید او را کنار می‌زدند. هیندنبرگ اصرار داشت که دو دسته از این فرمان معاف بمانند: یکی آن دسته از یهودیانی که در طول جنگ جهانی اول در ارتش خدمت کرده بودند، و دوم کسانی که پیش از شروع جنگ جهانی اول در یکی از مناصب دولتی استخدام شده بودند.

استادان دانشگاه جزء کارمندان دولت بحساب می‌آمدند، بنابراین آنها شامل این فرمان می‌شدند. از پنج استاد بزرگی که در گوتینگن مشغول تدریس بودند، سه تن از آنها یهودی بود (ادموند لاندو، ریچارد کورانت، فلیکس برون‌اشتاین)، چهارمی، هرمان وایل، همسری یهودی داشت. در میان استادان ریاضی، تنها گوستاو هرگولتز (Gustav Herglotz) بود که غیرقابل تصویه بود. در واقع فرمان 7 آوریل شامل لاندو و کورانت نمی‌شد، زیرا آنها تحت معافیت‌های هیندنبرگ قرار می‌گرفتند. لاندو در سال 1909 به سمت استادی رسیده بود؛ کورانت هم در جبهه غرب جنگیده بود.

البته در این جور موارد، نازی‌ها به نامه و قانون اکتفا نمی‌کردند. در آن زمان ساکنان شهر گوتینگن، چه دانشگاهی و غیر دانشگاهی، بیشتر طرفدار هیتلر بودند. در 1930 حزب نازی در گوتینگن بیش از دو برابر بقیه رای آورد. در آوریل 1926 روزنامه محلی شهر، Göttinger Tageblatt، که طرفدار نازی‌ها بود اعلام کرد که به شش استاد دانشگاه مرخصی نامحدود داده شده. این شش استاد از این خبر شگفت زده شدند، زیرا به خود آنها اطلاع داده نشده بود.

میان ماه‌های آوریل و نوامبر 1930، مرکز ریاضی دانشگاه گوتینگن از هم پاشید. این فقط شامل استادان یهودی نمی‌شد؛ هر کسی که تصور می‌شد کوچکترین تمایلات غیر-نازی دارد، مورد سوء ظن بود. ریاضیدانان از آنجا گریختند، و نهایتاً بیشتر آنها به آمریکا رفتند. روی هم رفته 18 استادِ ریاضی دانشگاه گوتینگن برکنار شده، یا آنجا را ترک کردند.

کسی که از ترک گوتینگن خودداری کرد ادموند لاندو بود (تنها استاد ریاضی گوتینگن که عضو کنیسه شهر نیز بود). لاندو که به درستی قانون تکیه داشت، تلاش کرد کلاس‌های حسابان خودش را در 1933 از سر بگیرد، ولی انجمن دانشجویان که از قصد او باخبر شده بود، کلاس‌های او را تحریم کرد. دانشجویان یونیفرم پوش مانع شدند تا بقیه دانشجویان به کلاس لاندو وارد شوند. لاندو که ناامید شده بود از رئیس انجمن دانشجویان نازی، که یک دانشجوی 20 ساله بنام اسوالد تایشمولر (Oswald Teichmüller) بود، خواست تا کتباً دلیل تحریم کلاس او را بیان کند. تایشمولر نیز اینکار را کرد، و این نامه اکنون موجود است.

تایشمولر مرد بسیار باهوشی بود که درواقع بعداً به یک ریاضیدان خوب بدل شد. از پاسخ او به لاندو روشن است که انگیزه او برای تحریم صرفاً جنبه ایدئولوژیک داشته. او قلباً و خالصانه به آرمان‌های نازی اعتقاد داشت، از جمله به بنیادی‌ترین آنها، و احساس می‌کرد دانشجویان آلمانی نباید توسط یهودی‌ها آموزش ببینند. اکثر ما پیش خودمان فکر می‌کنیم نازی‌ها‌ اشخاصی پست، بی‌شرف، و فرصت‌طلب بودند، و یا اگر هم هنرمند بودند، هنرمندانی شکست‌خورده بحساب می‌آمدند، که البته بیشتر آنها نیز چنین بودند. ولی باید خاطر نشان کرد که در میان آنها آدم‌هایی پیدا می‌شدند که از درجات بالایی از هوش و فراست برخوردار بودند [9].

لاندو که دل‌شکسته شده بود گوتینگن را ترک کرد. او به خانه خانوادگی خودش در برلین بازگشت، و از آنجا چندین سفر آموزشی به خارج از آلمان داشت، که از آنها خیلی لذت برد، ولی او وطنِ بومی خودش را ترک نکرد تا بطور دائم در خارج زندگی کند، و سرانجام در 1938 به مرگ طبیعی در خانه خودش در برلین درگذشت.

خود هیلبرت نیز در بحبوحه جنگ، در 14 فوریه 1943، بدنبال عارضه افتادن در خیابان، سه هفته بعد از تولد 81 سالگی‌اش، درگذشت. در تشیع جنازه او ده/دوازده نفر بیشتر شرکت نکرده بودند. از میان کسانی که در مراسم شرکت کردند فقط دو ریاضیدانانِ مهم بود: آرنولد زومرفیلد، که دوست قدیمی هیلبرت بود، و گوستاو هرگولتز که قبلاً از او نام بردم. شهر زادگاه هیلبرت، یعنی کوینسبرگ، بطور کامل در جنگ ویران شد؛ حالا این شهر در روسیه قرار دارد و کالینینگراد نامیده می‌شود. در حال حاضر گوتینگن یک دانشگاه معمولی در آلمان است، با یک بخش ریاضی قوی.

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

فصل 17

کمی نُکات جبری

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image006.png$

9/1/1401

1.

درواقع این کتاب باید شامل حجم زیادی از جبر باشد، خیلی بیشتر از آنچه تاکنون مطرح کرده‌‌ام. تمرکز من روی ریمان و کارهای او روی اعداد اول و تابع زتا بود. این کارها در حوزه نظریه اعداد و آنالیز بود، بنابراین روایت من هم بیشتر روی این موضوعات متمرکز بود. ولی همانطور که قبلاً اشاره کردم، ریاضیات نوین بسیار جبری است. در این فصل قصد دارم زمینه‌های جبری لازم برای درک دو رویکرد مهم در رابطه با فرضیه ریمان را برای شما توضیح دهم.

مانند فصول 7 و 15، این فصل نیز شامل دو فصل در یک فصل است. بخشهای 2 و 3 اصول نظریه میدان (field) را توضیح می‌دهد؛ در بخش‌های باقیمانده نیز نظریه عملگرها (operator theory) را بررسی خواهیم کرد. بسیاری از محققان بر این عقیده هستند که برای حمله به فرضیه اصلی ریمان، نظریه میدان بیشترین قدرت را دارد. بدنبال برخی تحولات قابل توجه‌ای که من بعداً شرح خواهم داد، نظریه عملگرها نیز اهمیت پیدا کرده. ولی ابتدا نظریه میدان.

2.

”میدان“ (Field) برای ریاضیدانان معنی ویژه‌ای دارد. اگر مطابق با قواعد عادی حساب ( مثلاً قاعده موسوم به شرکت‌پذیری: a×(b+c)=ab+ac ) عضوهای یک مجموعه بتوانند با هم جمع، تفریق، ضرب، و تقسیم شوند، آنگاه چنین مجموعه‌ای یک میدان را تشکیل می‌دهد. البته شرط مهم این است که نتیجه این عملیات نیز عضوی از مجموعه اولیه باشد.

مثلاً ℕ یک میدان نیست، زیرا اگر شما 12 را از 7 تفریق کنید، حاصل آن، یعنی −5، عضوی از ℕ نیست. بطور مشابه، اگر شما در $ℤ$ ، 12 را بر 7 تقسیم کنید، حاصل آن، یعنی $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image133.png$ ، عضوی از $ℤ$ نیست. بنابراین هیچکدام از این دو مجموعه میدان نیستند.

ولی ℚ، ℝ، و ℂ میدان هستند. اگر شما دو عدد گویا را با هم جمع، تفریق، ضرب، یا تقسیم کنید، حاصل یک عدد گویا خواهد بود. همین مورد برای اعداد حقیقی و مختلط صدق می‌کند. اینها سه نمونه از میدان هستند. البته هرکدام از آنها تعداد نامتناهی عضو دارند.

به سادگی می‌توان میدان‌های نامتناهی دیگری را ساخت. مثلاً اعدادی را درنظر بگیرید که بصورت $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image134.png$ هستند، که در آن a و b اعداد گویا هستند. در اینجا b یا صفر است یا صفر نیست. اگر b صفر نباشد، بدلیل اینکه $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image045.png$ یک عدد گویا نیست، $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image134.png$ نیز یک عدد گویا نخواهد بود. ولی مجموعه مورد نظر ما هم شامل اعداد گویا است و هم دسته خاصی از اعداد غیرگویا (ضرایب گویای $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image045.png$ )، بنابراین چنین مجموعه‌ای یک میدان است. اگر اعداد $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image134.png$ و $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image135.png$ را با هم جمع کنید حاصل آن $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image136.png$ است، اگر آنها را از هم تفریق کنید، حاصل آن $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image137.png$ است، اگر آنها را در هم ضرب کنید، حاصل آن $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image138.png$ است، و با استفاده از همان ترفندی که برای تقسیم اعداد مختلط از آن استفاده کردیم، اگر آنها را در بر هم تقسیم کنید، حاصل آن $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image139.png$ خواهد بود. بدلیل اینکه a و b می‌توانند کلیه اعداد گویا باشند، این میدان نیز بی‌نهایت عضو دارد.

یک میدان حتماً لازم نیست نامتناهی باشد. ساده‌ترین میدان ممکن، میدانی است با دو عضو 0 و 1. قاعده ضرب را برای آن چنین تعریف می‌کنیم: 0+0=0, 0+1=1, 1+0=1, 1+1=0. قاعد تفریق این است: 0−0=0, 0−1=1, 1−0=1, 1−1=0. (توجه داشته باشید که نتایج تفریق و جمع با هم یکسان هستند. هر علامت منفی در این میدان می‌تواند بطور آزاد با علامت مثبت جایگزین شود!) قواعد ضرب اینها هستند: 0×0=0, 0×1=0, 1×0=0, 1×1=1. قواعد تقسیم اینها هستند: 0÷1=0, 1÷1=1,، و تقسیم بر صفر مجاز نیست (تقسیم بر صفر هیچگاه مجاز نیست). این میدانِ کاملی است، و به هیچ وجه هم ساده نیست؛ من بعداً از آن استفاده خواهم کرد؛ ریاضیدانان این میدان را F₂ می‌نامند.

در واقع برای هر عدد اول، یا حتی برای همه توان‌های هر عدد اول، شما می‌توانید یک میدان متناهی تشکیل دهید. اگر p یک عدد اول باشد، یک میدان متناهی با p عضو، و p² عضو، و p³ عضو، و غیره وجود دارد. بعلاوه، اینها کلیه میدان‌های متناهی ممکن هستند. شما می‌توانید آنها را بصورت زیر فهرست کنید:

F², F⁴, F⁸, …, F³, F⁹, F²⁷,…, F⁵, F²⁵, F¹²⁵ ,… , F^p, F^p2, F^p3, …;

و اگر اینکار را کردید، شما کلیه میدان‌های متناهی ممکن را فهرست کرده‌اید (که تعداد آنها بی‌نهایت است).

خیلی از مبتدیان به اشتباه تصور می‌کنند که میدان‌های متناهی بیان مجدد حساب ساعتی هستند که من در بخش 8 فصل 6 به آن اشاره کردم. این تنها برای میدان‌‌هایی درست است که تعداد اعضای آنها یک عدد اول باشد. برای میدان‌های متناهی دیگر، حساب کمی پیچیده‌تر است. برای مثال، شکل 1-17 حساب ساعتی (شامل جمع و ضرب) را برای ساعتی که 4 شماره دارد نشان می‌دهد (یعنی اعداد 0، 1، 2، و 3).

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image140.png$

شکل 1-17. جدول‌های جمع و ضربِ ساعتی برای یک ساعت با 4-شماره. (در اینجا جمع و ضرب به طریق عادی انجام می‌شود، ولی وقتی حاصل عمل، عددی بزرگتر یا برابر 4 شد، باقیمانده تقسیم آن بر 4 را می‌گیریم.)

این دستگاهِ اعداد، و قواعد آن بسیار جالب و مفید است، ولی یک میدان نیست، زیرا شما نمی‌توانید اعداد 1 یا 3 را بر 2 تقسیم کنید. (اگر می‌توانستید اینکار را انجام دهید، آنگاه معادله 1=2×x جواب داشت، ولی مطابق با جدول ضرب بالا، چنین جوابی وجود ندارد.) از لحاظ ریاضی، این یک حلقه (ring) نامیده می‌شود (این اسم نامعقول بنظر نمی‌رسد، زیرا هر چه باشد ما درباره ساعت‌ها صحبت می‌کنیم). در یک حلقه شما می‌توانید جمع، تفریق، و ضرب را انجام دهید، ولی نه لزوماً تقسیم را.

حلقه خاصی که در شکل 1-17 نشان داده شده بود، دارای علامت رسمی ℤ/4ℤ است. باید اعتراف کنم که هیچ وقت این سبک از علامتگذاری‌ را دوست نداشته‌ام، بنابراین از حق نویسندگی خودم استفاده کرده، و برای این حلقه یک علامت می‌سازم: ℂ𝕃𝕆ℂ𝕂4 [10]. برای هر عدد طبیعی مانند N، شما به سادگی می‌توانید چنین حلقه‌ای را تشکیل دهید، که با علامتگذاری من، آن را بشکل ℂ𝕃𝕆ℂ𝕂N نشان می‌دهیم.

شما نمی‌توانید برای هر عدد طبیعی مانند N حلقه FN را تشکیل دهید. اینکار فقط برای Nهایی که عدد اول هستند، یا توان‌های آنها امکان دارد. برای یک عددِ اولِ خالص مثل p، Fp شبیه ℂ𝕃𝕆ℂ𝕂p است (با همان جداول جمع و ضرب). ولی برای توان‌های یک عدد اول، اوضاع کمی پیچیده‌تر می‌شود. جدول 2-17 جمع و ضرب را در F4 نشان می‌دهد. شما می‌بینید که F4 با ℂ𝕃𝕆ℂ𝕂4 فرق دارد:

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image141.png$

$شکل 2-17.$ $جمع و ضرب در میدان متناهی$ $F$ $4$ $.$

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

فصل 18

تلاقی نظریه اعداد و مکانیک کوانتوم

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image006.png$

13/1/1401

1.

در فصل قبل من به زمینه‌های ریاضی و تاریخی حدس هیلبرت-پولیا اشاره کردم. این حدس از زمان خودش خیلی جلوتر بود و تقریباً به مدت نیم قرن به فراموشی سپرده شد.

اما این نیم قرن دوران پرماجرایی در فیزیک بود، شاید پرماجراترین دورانی که فیزیک تا کنون بخودش دیده بود. در 1917، تقریباً در همان زمانی که حدسِ هیلبرت-پولیا مطرح شده بود، ارنست راترفورد شکاف اتم را مشاهده کرد؛ 15 سال بعد از آن، کاکرُفت و والتون با روش‌های مصنوعی اتم را شکافتند. این بنوبه خودش به کارهای انریکو فرمی انجامید، یعنی اولین واکنش زنجیره‌ای کنترل شده در 1942، و اولین انفجار هسته‌ای در 16 جولای 1945.

همانطور که خیلی از دبیران فیزیک می‌گویند، نامیدن این نوع واکنش‌ها به ”شکافِ اتمی“ اشتباه است، زیرا زمانی که شما یک کبریت را هم آتش میزنید، اتم‌ها از هم شکافته می‌شوند. منظور ما از شکافِ هسته اتم‌، مرکز اتم است. برای اینکه یک واکنش هسته‌ای داشته باشید (چه کنترل شده، چه کنترل نشده) شما باید یک ذره زیراتمی را به هسته یک اتم سنگین شلیک کنید. اگر اینکار را به روش خاصی انجام دهید، هسته‌ها شکافته می‌شوند، و بدنبال آن ذرات زیراتمی جدیدی را به بیرون شلیک می‌کنند. این ذرات به هسته‌های اتم‌های مجاور برخورد می‌کنند ... و با ادامه این فرایند ما یک واکنش زنجیره‌ای خواهیم داشت.

هسته یک اتمِ سنگین مخلوق بسیار عجیبی است. شما می‌توانید آن را مثل حباب جوشانی از پروتون‌ها و نوترون‌ها تصور کنید، که طوری به هم جوش خورده‌اند که شما نمی‌توانید بگویید بگویید سرو ته یک ذره کجاست. در عناصر بسیار سنگینی مثل اورانیم، کل حباب در آستانه ناپایداری قرار دارد.

همانطور که در اواسط قرن بیستم فیزیک هسته‌ای درحال توسعه بود، درک رفتار این مخلوقات عجیب، و بویژه فهم اینکه اگر یک ذره به آنها شلیک شود چه اتفاقی می‌افتد، بسیار پر اهمیت شد. این هسته یا حباب جوشان، می‌تواند در چند حالت وجود داشته باشد، که برخی دارای انرژی بالایی هستند (یک حباب جوشان پرانرژی) و برخی هم انرژی پایین (یک حباب جوشان راکد). اگر ذره‌ای به این هسته شلیک شود، طوری که هسته بجای اینکه از هم بپاشد آن را جذب کند، آنگاه (بدلیل اینکه انرژی ذره برخورد کننده باید جایی برود) هسته از یک حالت کم انرژی به حالتی بالاتر می‌رود. بعداً که از این حالت برانگیختگی خسته شد، ممکن است یک ذره معادل، یا یک ذره متفاوت، را از خودش گسیل کند، و به حالت انرژی پایین‌تر برود.

در چنین وضعیتی، چند سطح از انرژی امکان دارد؟ چه موقع یک هسته از سطح a به سطح b می‌رود؟ سطوح انرژی نسبت به یکدیگر چه فاصله‌ای دارند؟ و چرا فاصله آنها اینگونه است؟ سئوالاتی مثل این، مطالعه هسته را در حوزه بزرگتری از مسائل قرار داد: حوزه دستگاه‌های دینامیکی، یعنی مجموعه‌ای از ذرات که در هر نقطه از زمان، هر یک دارای یک مکان مشخص و یک سرعت مشخص هستند. همانطور که در دهه 1950 تحقیقات جلو می‌رفت، معلوم شد استفاده از آنالیز ریاضی در برخی از دستگاه‌های دینامیکی در مکانیک کوانتوم، از جمله هسته اتم‌های سنگین، کار را بیش از حد پیچیده‌ می‌کند. تعداد سطوح انرژی خیلی زیاد بود، و تعداد آرایش‌های ممکن نیز به مراتب بیشتر بود. کُل این وضعیت‌، شبیه کابوسی از مسئله ”چند-جسم“ در مکانیک کلاسیک بود (یعنی آنچه پیش از دوران کوانتوم مطرح بود). در مکانیک کلاسیک، چندین جسم (مثلاً سیارات یک منظومه خورشیدی) بودند که همه از طریق گرانش بر روی یکدیگر اثر داشتند.

برای پاسخ به این سطح از پیچیدگی، بکارگیری ریاضیاتِ دقیق با مشکل روبرو بود، بنابراین فیزیکدانان به آمار و احتمالات روی آوردند. اگر ما دقیقاً نتوانیم ببینیم چه اتفاقی می‌افتد، شاید بتوانیم ببینیم بطور میانگین احتمال دارد چه اتفاقی بی‌افتد. چنین رویکردهای آماری قبلاً بطور گسترده در مکانیک کلاسیک توسعه داده شده بودند و سابقه آن به سالهای 1850، یعنی خیلی پیش از زمانی که نظریه کوانتوم مطرح شود، بازمی‌گردد. اوضاع در جهان کوانتوم طور دیگری بود، ولی حداقل بخش مهمی از نظریه‌های کلاسیک بود که بتوان از آنها الهام گرفت. کارهای لازم انجام شده بود، ابزارهای آماری لازم برای دستگاه‌های دینامیک کوانتومی، مثل هسته اتم‌های سنگین، در اواخر دهه 1950 و اوایل دهه 1960 توسعه داده شدند. افراد کلیدی که در اینکارها نقش داشتند دو فیزیکدانِ هسته‌ای به نامهای یوجین ویگنر (Eugene Wigner) و فریمن دایسون (Freeman Dyson) بودند. یکی از مفاهیم اصلی کارهای آنها ماتریس‌ تصادفی (random matrix) بود.

2.

یک ماتریس تصادفی همان چیزی است که از اسم آن برمی‌آید، یعنی ماتریسی که اعضاء آن بطور تصادفی انتخاب شده‌اند. البته، نه کاملاً تصادفی. اجازه دهید نمونه‌ای از آنها را به شما نشان دهم. در زیر یک ماتریس 4×4 دیده می‌شود. این ماتریس از نوع خاصی است که من بعداً آن را توضیح می‌دهم. برای اینکه در فضا صرفه‌جویی کرده باشم، اعداد آن را به چهار رقم اعشار گرد کرده‌ام:

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image142.png$

اولین چیزی که ممکن است درباره این مثال متوجه آن شوید این است که ماتریس فوق یک ماتریس هرمیتی است (یعنی روی قطر اصلی خودش دارای تقارن است، به بخش 5 فصل 17 رجوع کنید). بخاطر دارید که یک ماتریس هرمیتی خواص زیر را دارد:

· با هر ماتریس N×N، یک چندجمله‌ای از درجه N متناظر است که چندجمله‌ای مشخصه ماتریس نامیده می‌شود.

· صفرهای چندجمله‌ای مشخصه، مقادیر ویژه ماتریس نام دارند.

· جمعِ مقادیر ویژه، رَد ماتریس نامیده می‌شود (که با مجموعِ اعضاء قطر اصلی ماتریس نیز برابر است).

· در یک حالت خاص از ماتریس‌های هرمیتی، مقادیر ویژه آن همگی حقیقی هستند، و بنابراین، ضرایب چندجمله‌ای مشخصه، و همچنین رَد ماتریس نیز اعداد حقیقی هستند.

چندجمله‌ای مشخصه ماتریسی که مثال زدم بصورت زیر است:

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image143.png$

که مقادیر ویژه آن عبارتند از: –3.8729، 0.0826، 1.5675، و 4.0864. رَد ماتریس 1.8636 است.

حالا توجه خودتان را به اعدادی معطوف کنید که ماتریس از آنها ساخته شده. اعدادی که در آنجا می‌بینید (کلیه اعداد مختلط غیر قطری، و اعداد حقیقی که قطر اصلی ماتریس را تشکیل داده‌اند) همگی به طریق خاصی تصادفی هستند. آنها گلچینی از اعداد تصادفی از یک توزیع گاوسی-نرمال هستند (همان منحنی ناقوس‌مانندی که در همه جای آمار دیده می‌شود).

فرض کنید که منحنی ناقوسی استاندارد را روی یک کاغذِ دقیقِ شطرنجی رسم کرده باشیم، طوری که صدها خانه مربع شکل زیر منحنی قرار گرفته باشند (شکل 1-18). یکی از این مربع‌ها را بصورت تصادفی انتخاب کنید؛ فاصله افقی آن از خط-مرکزی قله یک عدد تصادفی گاوسی-نرمال است.

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image144.png$

شکل 1-18. توزیع گاوسی-نرمال.

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

فصل 19

چرخاندن کلید طلایی

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image006.png$

17/1/1401

1.

حالا می‌خواهم تلاش کنم به قلب مقاله 1859 ریمان بروم. این شامل برخی عملیاتِ ریاضی است، که بسیار پیشرفته هستند. من سریعاً از بخش‌های دشوار می‌گذرم، و آنها را بعنوان کارهای انجام شده ارائه می‌دهم، و مثلاً با گفتن ”ریاضیدانان روشی برای بدست آوردن این نتیجه دارند“، فقط سعی می‌کنم مراحل منطقی استدلال ریمان را توضیح دهم، و از گفتن جزئیات این روش‌‌ها، یا اینکه چرا جواب می‌دهند، صرف نظر می‌کنم.

امید من این است که حداقل شما مراحل اصلی که ریمان دنبال کرده بود را درک کنید. ولی حتی انجام اینکار هم به استفاده اندکی از حسابان نیاز دارد. اینها شامل همان نکات اساسی می‌شوند که من در بخش‌های 6 و 7 فصل 7 بیان کردم. ممکن است برخی از بخش‌های آتی این فصل دشوار بنظر برسد. ولی پاداشی که در انتها نصیب شما خواهد شد، درک زیبایی و قدرتی است که به دنبال دارد، یعنی فرضیه ریمان، اهمیت آن، و ارتباط آن با توزیع اعداد اول.

2.

برای شروع، من تا حدی قصد دارم چیزی که در بخش 4 فصل 3 گفتم را رد کنم. در آنجا من گفتم فایده‌ای ندارد نمودار تابع شمارشِ اعداد اول، یعنی π(N) را رسم کنیم. در آنجا فایده‌ای نداشت، ولی اینجا دارد.

ولی ابتدا می‌خواهم تعدیل‌های اندکی را انجام دهم. بجای نوشتن π(N)، که از نظر ریاضیدانان به معنی ”تعداد اعداد اولی است که کمتر یا مساوی عدد طبیعی N هستند“، من می‌خواهم بنویسم π(x)، که یعنی ”تعداد اعداد اولی که کمتر یا مساوی عدد حقیقی x هستند“. این چیز مهمی نیست. معلوم است که اعداد اولی که کمتر یا مساوی 37.51904283 هستند، همان‌هایی هستند که کمتر یا مساوی 37 هستند، یعنی: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37. ولی بدلیل اینکه ما می‌خواهیم بسوی حسابان برویم، به ناچار باید از اعداد حقیقی استفاده کنیم، و نه صرفاً از اعداد طبیعی.

تعدیل دیگری نیز باید انجام گیرد. همانطور که در یک محدوده از مقادیر، من به آرامی آرگومان x را افزایش می‌دهم، π(x) ناگهان پرش می‌کند. مثلاً فرض کنید x در محدوده 10 تا 12 به آرامی افزایش یابد. تعداد اعداد اول کوچکتر از 10 برابر 4 است (2، 3، 5، و 7)، بنابراین وقتی x=10 باشد مقدار تابع برابر 4 است، و البته این درمورد x=10.1، x=10.2، x=10.3، و غیره هم صادق است. ولی موقعی که x به 11 می‌رسد، ناگهان مقدار تابع به 5 جهش می‌کند؛ و این برای 11.1, 11.2, 11.3, … نیز صادق است و مقدار تابع روی 5 ثابت می‌ماند. این چیزی است که ریاضیدانان به آن یک تابع پله‌ای (step function) می‌گویند. تعدیلی که از آن صحبت کردم بیشتر برای توابع پله‌ای متداول است، به این صورت که دقیقاً در همان نقاطی که π(x) پرش می‌کند، من مقدار½ را از آن کم می‌کنم. بنابراین برای آرگومان‌های 10.9، یا10.99 ، یا 10.999999، مقدار تابع 4 است، برای آرگومان‌های 11.1، یا 11.01، یا 11.000001 مقدار تابع 5 است، ولی برای خود 11 (که ناگهان پرش رخ داده) مقدار تابع 4.5 می‌باشد. اگر چنین چیزی غیرعادی بنظر می‌رسد مرا ببخشید، ولی برای آنچه در ادامه می‌آید، اینکار ضروری است. استدلالات این فصل و فصل 21 تنها در صورتی جواب خواهند داد که من اینکار را انجام دهم، و اگر نکنم آنها جواب نمی‌دهند.

حالا من می‌توانم نمودار π(x) را رسم کنم (شکل 1-19 را ببینید). در ابتدا عادت کردن به توابع پله‌ای دشوار است، ولی از لحاظ ریاضی آنها کاملاً بامعنی هستند. در اینجا دامنه تابع کلیه اعداد غیر منفی است. در این دامنه، هر آرگومانی دارای یک مقدارِ تک است. هر آرگومانی را که به من بدهید، من هم برای این تابع یک مقدار را به شما می‌دهم. در ریاضیات توابعی هستند که از این هم بسیار عجیب‌ترند.

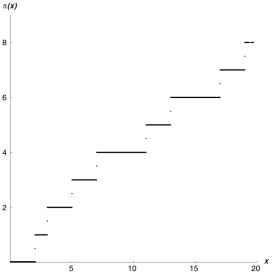
$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image145.png$

شکل 1-19. نمودار تابع شمارش اعداد اول، π(x).

3.

حالا می‌خواهم تابع پله‌ای دیگری را به شما معرفی کنم که کمی از π(x) عجیب‌تر است. ریمان در مقاله 1859 خودش نام این تابع را ”f“ گذاشته بود، ولی می‌خواهم از هارولد ادواردز (Harold Edwards) پیروی کرده و آن را تابع ”J“ بنامم. از زمان ریمان به بعد، ریاضیدانان عادت دارند از ”f“ برای نشان دادن یک تابعِ عام استفاده کنند، و مثلاً می‌گویند: ”فرض کنید f هر تابعی باشد که ...“، بنابراین برای آنها مشکل است که از f برای نشان دادن تابع خاصی استفاده کنند.

بسیار خوب، در زیر تعریف تابع J را می‌بینید. برای کلیه اعداد غیر منفی x، تابع J مقداری را به ما می‌دهد که در عبارت 1-19 نشان داده شده:

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image146.png$

عبارت 1-19. تعریف تابع J.

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

فصل 20

عملگر ریمان و رویکردهای دیگر

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image006.png$

19/1/1401

1.

قانون مونتگومری- اودلیزکو به ما می‌گوید که صفرهای غیر-ساده تابع زتای ریمان، بطور آماری شبیه مقادیر ویژه برخی ماتریس‌های تصادفی هرمیتی هستند. از عملگرهایی که توسط چنین ماتریس‌هایی نشان داده می‌شوند، می‌توان برای مدل‌سازی برخی از دستگاه‌های دینامیکِ کوانتومی استفاده کرد. بنابراین، آیا عملگری هست که مقادیر ویژه آن دقیقاً صفرهای تابع زتا باشد؟ اگر هست، نشان دهنده چه نوع دستگاه‌ دینامیکی است؟ آیا چنین سیستمی را می‌توان در یک آزمایشگاه فیزیک ایجاد کرد؟ و اگر بتوان اینکار را کرد، این چه سودی برای اثبات فرضیه ریمان دارد؟

حتی پیش از اینکه مقاله 1987 اودلیزکو منتشر شوذ، تحقیق درباره این سئوالات در حال انجام بودند. در واقع سال پیش از آن، فیزیکدان انگلیسی مایکل بِری (Michael Berry) با استفاده از نتایجی که در آن زمان بطور گسترده در دسترس بودند، از جمله برخی از کارهای اودلیزکو، مقاله‌ای را منتشر کرد با عنوان ”آیا تابع زتای ریمان می‌تواند مدلی برای آشوب کوانتومی باشد؟“ بِری به سئوالات زیر پرداخت: فرض کنید چنین عملگرِ ریمانی وجود داشته باشد، در اینصورت چه نوع دستگاه دینامیکی را مدل‌سازی می‌کند؟ پاسخ او این بود: یک دستگاه آشوبناک (Chaotic). برای توضیح این موضوع من باید گریزی به نظریه آشوب (Chaos Theory) بزنم.

2.

ارتباط نظریه اعدادِ محض (یعنی ایده‌های مربوط به اعداد طبیعی و ارتباط آنها با یکدیگر) با فیزیک ذرات اتمی خیلی تعجب برانگیز نیست. فیزیک کوانتوم نسبت به فیزیک کلاسیک دارای مؤلفه‌های حسابی قوی‌تری است، زیرا به این ایده تکیه دارد که ماده و انرژی بصورت بی‌نهایت قابل تقسیم نیستند. انرژی به صورت پیمانه‌های (quanta) 1تایی، 2تایی، 3تایی ، یا 4تایی می‌آید، و نه 1½ تایی ، $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image147.png$ تایی ، $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image045.png$ تایی ، یا π تایی. ولی این پایان ماجرا نیست، مکانیک کوانتم بدون بهره‌گیری از قویترین ابزارهای آنالیز مدرن امکان پیشرفت نداشت. برای مثال، فرمول معروف شرودینگر، معروف به معادله موج، به زبان حسابان سنتی نوشته شده. بااینحال، مؤلفه‌های حسابی در مکانیک کوانتوم وجود دارد، درحالیکه در مکانیک کلاسیک کاملاً غایب هستند.

بنیان‌های فیزیکِ کلاسیک (یعنی فیزیکِ نیوتونی و اینشتینی) از لحاظ ریاضی اساساً آنالیتیک هستند، که یعنی آنها بر آنالیز ریاضی، بر مفهوم تقسیم‌پذیری بی‌انتها، بر همواری و پیوستگی، و بر حدود و مشتقاتِ اعداد حقیقی تکیه دارند. بخاطر داشته باشید که نیوتون علاوه بر مکانیک کلاسیک، حسابان را نیز اختراع کرد، چیزی که نهایتاً بیشتر آنالیز را تحت الشعاع قرار داد.

برای نمونه، مسئله کلاسیک دو جسم را در نظر بگیرید: دو جسم در یک مدار بیضی شکل به دور یکدیگر در حال گردش هستند، و هر دو آنها تحت گرانش یکدیگر قرار دارند. اگر این دو جسم در فاصله معینی از یکدیگر قرار داشته باشند (که با r که یک عدد حقیقی است اندازه‌گیری می‌شود)، جسم کوچکتر سرعت معینی دارد (که با v که باز هم یک عدد حقیقی است اندازه‌گیری می‌شود). رابطه میان r و s توسط یک عبارت دقیق ریاضی بیان می‌شود؛ در واقع v تابعی از r است، که توسط معادله زیر بیان می‌شود:

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image148.png$

که در آن M و a اعداد ثابتی هستند که توسط برخی مؤلفه‌ها و شرایط اولیه سیستمِ مورد نظر (مثل جرم دو جسم، و غیره) تعیین می‌شوند.

البته ما در عمل نمی‌توانیم اعدادی با دقت بینهایت (یعنی اعداد حقیقی) را به r و v نسبت دهیم. ممکن است مثلاً ما بتوانیم r را با دقت 10، یا حتی 20 رقم اعشار اندازه‌گیری کنیم؛ ولی برای مشخص کردن یک عدد حقیقی شما به تعدادِ بی‌نهایتی از ارقامِ اعشاری نیاز دارید، و ما نمی‌توانیم به چنین چیزی برسیم. بنابراین، اگر با یک مسئله عینی واقعی مواجه باشیم، تخصیص یک عدد حقیقی برای r، خواه و ناخواه با کمی خطا همراه است، و همین موجب می‌شود مقداری که برای v محاسبه می‌شود نیز با خطای مشابه‌ای همراه باشد. این مشکل بزرگی نیست. قوانین کپلر به ما اطمینان می‌دهند که آنچه ما خواهیم داشت، در هر حال یک مدار بیضی شکل است، و ریاضیات به ما می‌گوید که اگر در اندازه‌گیری r یک درصد خطا داشته باشیم، این در مقدار محاسبه شده برای v فقط به اندازه 0.5 درصد انعکاس خواهد داشت. چنین وضعیت‌هایی قابل پیش‌بینی و قابل‌کنترل هستند. اینها چیزهایی‌ هستند که ریاضیدانان به آنها ”انتگرال‌پذیر“ می‌گویند.

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

فصل 21

جمله خطا

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image006.png$

25/1/1401

1.

در فصل 19، پس از اینکه تابع پله‌ای J(x) را بر حسب تابع شمارنده اعداد اول، یعنی π(x)، تعریف کردم، از معکوس‌سازی موبیوس استفاده کردم تا π(x) را بر حسب J(x). بگیرم. سپس با چرخاندن کلید طلایی، مراحلی را طی کردم که ریمان برای گرفتن تابع ζ(x) بر حسب J(x) آنها را پیموده‌ بود. اینها را می‌شود بصورت زیر خلاصه کرد:

· تابع شمارنده اعداد اول، یعنی π(x)، می‌تواند بصورت جملاتی از تابع پله‌ای J(x) بیان شود.

· تابع J(x) می‌تواند بر حسب تابع زتای ریمان، یعنی ζ(x)، بیان شود.

بنابراین، می‌توان نتیجه گرفت که کلیه خواص تابع شمارند اعداد اول، π(x)، به نحوی در خواص تابع زتا ζ، پنهان شده‌اند. با انجام یک مطالعه دقیق روی ζ، آنچه را که می‌خواهیم درباره π بدانیم به ما خواهد گفت، به عبارت دیگر، چگونگی توزیع اعداد اول را برای ما مشخص خواهد کرد.

ولی چگونه چنین چیزی ممکن است؟ این چیزی که پنهان شده چیست؟ این صفرهای غیر-ساده چطور با آن ارتباط دارند؟ و آن تابع واسطه، یعنی J(x)، وقتی برحسب ζ نوشته شود چه شکلی خواهد داشت؟ این همان موضوعی است که در پایان فصل 19 آن را رها کردم.

2.

من برای رها کردن این موضوع دلیل خیلی خوبی داشتم، که در ادامه این بخش روشن خواهد شد. در عبارت 1-21 نتیجه آخرین معکوس‌سازی نشان داده شده. این همان عبارت دقیق و نهایی برای J(x) است که برحسب ζ نوشته شده:

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image149.png$

عبارت 1-21.

عبارت بالا، اگر ریاضیدان نباشید عبارت زمخت و پیچیده‌ای بنظر می‌رسد (ضمناً، تابع زتا در کجای این عبارت قرار دارد؟) من می‌خواهم این عبارت را تکه تکه کرده و به شما نشان دهم که در درون آن چه می‌گذرد. پیش از هر چیزی می‌خواهم اشاره کنم که این معادله همان نتیجه اصلی است که در مقاله اصلی 1859 ریمان آمده بود. اگر بتوانید نوعی بینش را نسبت به آن کسب کنید، اساساً کاری که ریمان در این حوزه انجام داد را درک خواهید کرد و چشم‌انداز روشنی از پی‌آمدهای آن خواهید داشت.

اولین چیزی که باید به آن توجه داشته باشید این است که سمت راست عبارت 1-21 دارای چهار بخش یا جمله است. اولین جمله Li(x) است، که کلاً ”جمله اصلی“ نامیده می‌شود. بنا به دلایلی که به زودی معلوم خواهد شد، ریمان از جمله دوم $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image150.png$ بعنوان ”جملات متناوب“ نام می‌برد، ولی من فقط بعنوان ”جمله دوم“ از آن نام می‌برم. جمله سوم هم که بسیار ساده است. این فقط یک عدد ثابت است که مقدار آن برابر 0.69314718055994… است.

جمله چهارم هر چند از نظر غیر-ریاضیدانان ممکن است ترسناک بنظر برسد، ولی به آسانی می‌توان از آن صرف نظر کرد و آنرا دور انداخت! این یک انتگرال است، یعنی مساحت زیر منحنی یک تابع معین، که از آرگومان x تا بی‌نهایت اندازه‌گیری می‌شود. این تابع $Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image151.png$ است. اگر شما نمودار این تابع را رسم کنید (شکل 1-21)، خواهید دید که برای منظور فعلی ما بسیار روان بنظر می‌رسد.

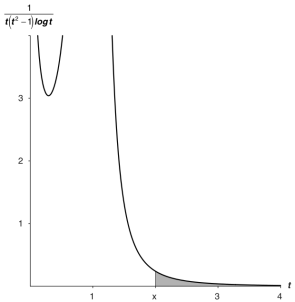
$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image152.png$

شکل 1-21. نمودار جمله چهارم عبارت ریمان برای J(x)..

توجه داشته باشید که در J(x) ، ما هیچ علاقه‌ای به آرگومان‌هایی که در آنها x کوچکتر از 2 باشد نداریم، زیرا وقتی x<2 باشد، مقدار J(x). هم صفر است. بنابراین من ناحیه‌ای از این مساحت که با x=2 متناظر است را با رنگ تیره نشان داده‌ام تا شما ببینید این انتگرال (که جمله چهارم را تشکیل می‌دهد) تا چه اندازه می‌تواند کوچک و تاثیرگذار باشد. مقدار واقعی این سطح، یعنی حداکثر مقداری که جمله چهارم برای تمام xهایی که برای ما جالب هستند ممکن است بگیرد 0.1400101011432869… است.

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

فصل 22

یا درست است، یا درست نیست

$Description: Description: Description: C:\Users\kami\Documents\My Books\PRIME OBSESSION\sum_files\image006.png$

31/1/1401

1.

بعد از گذشت 120 سال که فرضیه ریمان مورد توجه ریاضیدانان بوده، حالا این خشنودی وجود دارد که توجه فیزیکدانان را نیز به خودش جلب کرده. همانطور که در بخش 1 فصل 10 گفتم، افکار ریمان بسیار به افکار یک فیزیکدان شباهت داشت. لاوگویتس (Laugwitz) می‌گوید ” از نه مقاله‌ای که او منتشر کرد، باید چهار تای آنها را به فیزیک متعلق دانست.“ در واقع متخصص نظریه اعداد آلمانی، اولریخ ورهاور (Ulrike Vorhauer)، به من یاد یادآور شد که در زمان ریمان تمایز چندانی بین یک ریاضیدان و فیزیکدان وجود نداشت. تا کمی پیش از ریمان، چنین تمایزی اصلاً وجود نداشت. گاوس یک فیزیکدان تراز-اول و همینطور یک ریاضیدان تراز-اول بود و اگر می‌شنید که این دو رشته جدا از هم هستند، آشفته می‌شد.

جاناتان کیتینگ (Jonathan Keating) برای من داستان زیر را نقل کرد، که باید بگویم از نظر من تا حدی وهم‌آور بود:

من و یکی از همکاران خودم مشغول گذراندن تعطیلات در کوهستان‌های هارز (Harz) آلمان بودیم. ما تصمیم گرفتیم با ماشین به دانشگاه گوتینگن، که در 50 کیلومتر ما قرار داشت، برویم. ما می‌خواستیم به کتابخانه دانشگاه رفته و نگاهی به یادداشت‌های کاری ریمان بی‌اندازیم. من خودم قصد داشتم یادداشت‌های او که مربوط به حوالی سال‌های 1859 و درباره تابع زتا بود را بررسی کنم.

ولی همکارم که یک ریاضیدانِ کاربردی بود اصلاً علاقه‌ای به نظریه اعداد نداشت، و فقط می‌خواست کارهای کاملاً متفاوتی از ریمان که به اختلال (perturbations) مربوط بود را بررسی کند. حباب بزرگی از گاز را تصور کنید که در یک فضای خالی قرار دارد. اگر ضربه موثری به آن وارد آورید چه اتفاقی می‌افتاد؟ خوب، اساساً احتمال دارد دو اتفاق بی‌افتاد: ممکن است از هم بپاشد، یا ممکن است با فرکانس خاصی شروع به لرزش کند. این به اندازه، جهت، و مکان ضربه، و شکل و اندازه حباب اولیه و غیره بستگی دارد.

ما به کتابخانه رسیدیم، و من از مسئول مربوطه خواستم یادداشت‌های ریمان درباره نظریه اعداد را برای من بیاورد. همکارم نیز درخواست کرد یادداشت‌های مربوط به نظریه اختلال را برای او بیاورند. پس از بررسی‌هایی که کتابدار انجام داد، او پیش ما بازگشت و گفت که یک مجموعه واحد از یادداشت‌های ریمان هست که نیاز هر دو ما را برآورده می‌کند. این نشان می‌دهد که او همزمان بر روی هر دو این مسائل مشغول کار بوده.

جاناتان اضافه کرد که البته ریمان ابزارهای قرن بیستمی، مانند جبر عملگرها، را در دسترس نداشت تا برای حل مسائل اختلال از آنها استفاده کند. او فقط از معادلات دیفرانسیل استفاده می‌کرد، و نوعی عملگرهای ابتدایی را نیز برای خودش ابداع کرده بود. با اینحال، هنوز مشکل می‌توان باور کرد که شخصی به تیزهوشی ریمان چگونه می‌توانسته متوجه شباهت میان صفرهایی که روی خط مرزی قرار دارند، و طیف فرکانس‌های اختلال نشده باشد. 113 سال بعد، این شباهت خودش را بصورت فاحشی در یک مهمانی عصرانه نشان داد.

2.

آنچه از قول کیتینگ بیان کردم، مربوط به یک گردهم‌آیی بود که در سال 2002 و در موسسه کورانت دانشگاه نیویورک برگذار می‌شد. این کنفرانس چهار روزه‌ای‌ بود، که از طرف موسسه ریاضی آمریکا (AIM) ترتیب داده شده بود. عنوان یکی از آنها ”کارگاه مربوط به تابع زتا و فرضیه ریمان“ بود.

در سالن کنفرانس موسسه کورانت اشخاص بسیار معروفی حضور داشتند. از معروف‌ترین کسانی که در آنجا دیده می‌شد آلته سلبرگ بود. او در آن زمان 84 ساله بود و هنوز بسیار تیز و هشیار بنظر می‌رسید (در واقع او بر سر یک مسئله تاریخی مربوط به ریاضیات، پیتر سارناک، که 36 سال از او جوانتر بود، و یکی از ریاضیدانان مطرح بود آن زمان بود، را به چالش کشیده بود. هنگام استراحت برای نهار، من به کتابخانه رفتم و نکته‌ای که سلبرگ گفته بود را بررسی کردم، و دیدم حق با او بود.) بسیاری از اشخاص معروف دیگر نیز در آنجا حضور داشتند، از جمله افرادی که در چند فصل اخیر از آنها نام بردم: مونت‌گومری، اودلیزکو، یا اندرو وایلز (Andrew Wiles) که در آن زمان به خاطر اثبات آخرین قضیه فرما یک فوق‌ستاره بحساب می‌آم، هارولد ادواردز که نویسنده کتاب معروفی درباره تابع زتا است، و من چندین بار در این کتاب از او نام بردم، و دانیل بامپ (Daniel Bump) که یکی از دو نفری است که نام او با قضایای مربوط به فرضیه ریمان بسیار گره خورده.

طی سال‌های اخیر، موسسه ریاضی آمریکا یکی از نیروهای موثر در حمله به فرضیه ریمان بوده. کنفرانس کورانت سومین کنفرانسی بود که آنها در رابطه با موضوعات مربوط به فرضیه ریمان برگذار می‌کردند. اولین کنفرانس در سال 1996 در واشینگتن بود که به مناسبت گرامی‌داشت یک صدمین سال اثبات قضیه اعداد اول توسط آدامار و دو لا والی پوسان برگذار شد. دومین کنفرانس در 1998، در موسسه اروین شرودینگر وین برگذار شد. فعالیت‌های AIM به هیچ وجه محدود به مطالعات مربوط به فرضیه ریمان، یا حتی نظریه اعداد، نبود. مثلاً، در حال حاضر، آنها پروژه‌ای را دارند که به نسبیت عام مربوط است. ولی کار مهمی که آنها انجام می‌هند، گرد هم آوردن دانشمندان حوزه‌های مختلف، و دنبال کردن رویکردهای مختلف برای حل مسائل است. مثلاً رویکردهای جبری، آنالیزی، محاسباتی، و فیزیکی.

AMI در سال 1994 توسط ریاضیدان مطرح آمریکایی جرالد آلکساندرسون (Gerald Alexanderson) و بازرگان کالیفرنیایی، جان فرای (John Fry) تاسیس شد. جان از یک خانواده کارآفرین می‌آمد. پدر و مادر او صاحب یک فروشگاه زنجیره‌ای موفق در کالیفرنیا بودند. جان از اوایل دهه 1970 عاشق ریاضیات شد و در همین رشته از دانشگاه سانتا کلارا، که الکساندرسون هم عضو هیئت علمی آنجا بود، فارغ‌التحصیل شد. جان پس از فارغ‌التحصیلی با این انتخاب روبرو بود که آیا به دنبال کسب و کار خانوادگی خودش برود یا تحصیل ریاضیات را دنبال کند. او تجارت را انتخاب کرد و به همراه برادرانش در کالیفرنیا فروشگاه‌های زنجیره‌ای Fry’s Electronics را راه‌اندازی کردند، که بعداً به سراسر آمریکا گسترش یافت.

جان فرای و جری الکساندسون با هم در تماس بودند. آنها یک علاقه مشترک داشتند، و آن جمع آوری کتاب‌های کمیاب ریاضی و نسخه‌های اصلی مقالات بود. در اوایل دهه 1990 آنها تصمیم گرفتند با استفاده از کلکسیون خودشان یک کتابخانه تاسیس کنند. این تصمیم به طرحی برای تاسیس یک موسسه بدل شد. آنها برای اینکار یکی از هم‌کلاسی‌های قدیمی جان بنام برایان کانری (Brian Conrey) را دعوت به همکاری کردن. کانری یک متخصص نظریه اعداد و رئیس بخش ریاضی دانشگاه ایالتی اوکلاهوما بود.

در سال‌های ابتدایی تاسیس خودش، موسسه ریاضی آمریکا تقریباً بطور کامل با سرمایه شخصی جان فرای اداره می‌شد، که چیزی در حدود سیصد هزار دلار در سال می‌شد. این نمونه خوبی از انجام یک کار خیر بصورت پنهانی بود. جان مرد تودار و خلوت گرایی است که زندگی و فعالیت‌های خودش را عمومی نمی‌کند. وقتی من برای اولین بار درباره موسسه ریاضی آمریکا شنیدم، در اینترنت نام او را جستجو کردم، تا شاید عکسی از او پیدا کنم [11]؛ ولی چنین چیزی موجود نبود. ولی او در محیط مورد علاقه خودش، یعنی در میان ریاضیدانان و علاقه‌مندان به ریاضی، بطور کامل در دسترس بود. او در نیویورک به مناسبت کنفرانس کورانت یک مهمانی نهار ترتیب داد، که من هم در آن حضور داشتم. مردی بلند قد با صورتی پسرانه که وقتی درباره ریاضیات صحبت می‌کرد شاد بنظر می‌آمد. من در شگفت بودم که آیا او از تصمیم خودش برای انتخاب تجارت بجای دانشگاه، هیچ وقت پشیمان شده بود یا نه، ولی چنین سئوالی ممکن بود گستاخانه بنظر برسد، و من هم فرصت پرسیدن آن را از دست دادم.

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

[1] - زبان اسلاو، زبان چند کشور شرق اروپا است، که بزرگترین آنها روسیه و اوکراین می‌باشد (مترجم).

[2] - خواننده لغتهای ”روس“ و ”پروس“ را با هم اشتباه نگیرد. پروس یک ناحیه تاریخی بود که شامل نواحی شرقی آلمان امروزی، لهستان، و برخی نواحی غربی روسیه امروز می‌شود. پروس در اواخر قرن نوزدهم منحل شد (مترجم).

[3] - نبرد مهمی که در سال 1815 در نزدیکی بروکسل رخ داد و نیروهای انگلیس و پروس بر علیه ناپلئون جنگیدند و فرانسه را شکست دادند. این آخرین شکست ناپلئون بود و پس از آن دیگر هیچگاه قدرت پیشین خود را بازنیافت (مترجم).

[4] - اشاره به سوفی ژرمن ریاضیدان زن فرانسوی است، که از ژنرال فرانسوی خواست هیچ آسیبی به گاوس نزند (مترجم).

[5] - تعریف ریشه سوم x، عددی است که اگر آن را بتوان 3 برسانیم، حاصل آن x شود.

[6] - بیمارانی بدحالی که نبض‌شان را از دست می‌هند، نمودار قلبی آنها به شکل یک خط افقی ثابت ظاهر می‌شود (مانند نمودار x⁰)، که اگر فوراً احیاء نشوند، این وضعیت می‌تواند به مرگ منتهی شود (مترجم).

[7] - همسر نویسنده کتاب، جان داربی‌شر، متولد چین است (مترجم).

[8] - در زبان انگلیسی از many برای اشاره به چیزهای شمردنی، و از much برای چیزهای غیر شمردنی استفاده می‌شود. معنی سئوال بچه در جمله ”How much presents did you get?“ این است که ”چقدر کادو گرفتی؟“ در صورتی صحیح‌تر آن این است که بجای much از many استفاده کند و بگوید چندتا کادو گرفتی (مترجم).

[9] - روشن است یکی از کسانی که نویسنده در اینمورد به آنها نظر دارد تایشمولر است. در واقع تایشمولر ریاضیدان جوانی بود که فقط 30 سال زندگی کرد و نهایتاً جان خودش را فدای آرمان‌های (غلط) خودش کرد. او در 1943 در جبهه غربی کشته شد، ولی در همین مدت کوتاه، او از لحاظ ریاضی توانست دست‌آوردهای قابل توجه‌ای را کسب کند. فضای تایشمولر (Teichmüller space) که به افتخار او نامگذاری شده، 70 سال پس از مرگش، درواقع یکی از حوزه‌های تحقیقاتی ریاضیدان فقید ایرانی، مریم میرزاخانی بود (مترجم).

[10] - خواننده متوجه است که منظور نویسنده از ℂ𝕃𝕆ℂ𝕂 ساعت، و حساب ساعتی است.

[11] - امروزه انسان‌های ثروتمند و خَیر زیادند، و در میان آنها کسانی که متخصص و آینده‌نگر هستند شاخص‌ترند. در دوران فعلی، می‌توان به اشخاصی مانند ایلان ماسک یا جف بزوس اشاره کرد. اگر رشد اقتصادی آنها به همین منوال ادامه پیدا کند، احتمال داده می‌شود که ایلان ماسک اولین کسی باشد که در آینده عنوان تریلیاردر را می‌گیرد (البته به شرط رسیدن ثروت او به یک تریلیون دلار، و گرنه ما در کشور خودمان خیلی وقت است ثروتمندان تریلیاردر تومانی داریم!). من به هیچ وجه قصد ندارم ارزش تلاشهای کسانی مثل ایلان ماسک را دست کم بگیرم، و اگر هم در جهان افراد فوق ثروتمندی وجود دارند، امیدوارم حداقل مانند او دانشمند و آینده‌نگر باشند. از نظر من، چنین اشخاصی با رویاهایی که در سر دارند و با پولی که در جیبشان هست، موتور محرکه پیشرفت انسان هستند. ولی چیزی که مایلم در اینجا به آن اشاره کنم مقام انسانی آنها است. اول اینکه انگیزه اولیه کسانی مثل ماسک یا بزوس افزایش سرمایه است و انگیزه‌های دیگر، در مراتب بعدی قرار می‌گیرد. در صورتی که برای کسانی مثل جان فرای، صرفاً پیشرفت انسان بطور کلی، و پیشرفت ریاضیات بطور اخص اهمیت دارد. اگر روزی فرضیه ریمان، یا دیگر مسائلِ چالش‌برانگیز ریاضی حل شود، چه سودی نصیب این اشخاص خواهد شد؟ هیچ! آنها فقط خشنود خواهند شد. کسانی مثل فرای آنقدر عزت نفس دارند که حتی نمی‌خواهند اسم آنها مطرح شود. در مقابل، کسانی مثل ماسک را در نظر بگیرید که هر روز جلوی دوربین ظاهر شده و ادا و اطوار درمی‌آورند، گویی هنوز یک پسر دوازده ساله هستند که بزرگ نشده‌ و فقط ذوق اسباب‌بازی‌های خودشان را می‌کنند (مترجم).

Like: ,

2	3	4	5	6	7	8	9	10	11	12	13	14	15
16	17	18	19	20	21	22	23	24	25	26	27	28	29
30	31	32	33	34	35	36	37	38	39	40	41	42	43
44	45	46	47	48	49	50	51	52	53	54	55	56	57
58	59	60	61	62	63	64	65	66	67	68	69	70	71
72	73	74	75	76	77	78	79	80	81	82	83	84	85
86	87	88	89	90	91	92	93	94	95	96	97	98	99

2	3	.	5	.	7	.	9	.	11	.	13	.	15
.	17	.	19	.	21	.	23	.	25	.	27	.	29
.	31	.	33	.	35	.	37	.	39	.	41	.	43
.	45	.	47	.	49	.	51	.	53	.	55	.	57
.	59	.	61	.	63	.	65	.	67	.	69	.	71
.	73	.	75	.	77	.	79	.	81	.	83	.	85
.	87	.	89	.	91	.	93	.	95	.	97	.	99
.	101	.	103	.	104	.	107	.	109	.	111	.	113

2	3	.	5	.	7	.	.	.	11	.	13	.	.
.	17	.	19	.	.	.	23	.	25	.	.	.	29
.	31	.	.	.	35	.	37	.	.	.	41	.	43
.	.	.	47	.	49	.	.	.	53	.	55	.	.
.	59	.	61	.	.	.	65	.	67	.	.	.	71
.	73	.	.	.	77	.	79	.	.	.	83	.	85
.	.	.	89	.	91	.	.	.	95	.	97	.	.
.	101	.	103	.	.	.	107	.	109	.	.	.	113

2	3	.	5	.	7	.	.	.	11	.	13	.	.
.	17	.	19	.	.	.	23	.	.	.	.	.	29
.	31	.	.	.	.	.	37	.	.	.	41	.	43
.	.	.	47	.	49	.	.	.	53	.	.	.	.
.	59	.	61	.	.	.	.	.	67	.	.	.	71
.	73	.	.	.	77	.	79	.	.	.	83	.	.
.	.	.	89	.	91	.	.	.	.	.	97	.	.
.	101	.	103	.	.	.	107	.	109	.	.	.	113

2	3	4	5	6	7	8	9	10	11	12	13	14	15
16	17	18	19	20	21	22	23	24	25	26	27	28	29
30	31	32	33	34	35	36	37	38	39	40	41	42	43
44	45	46	47	48	49	50	51	52	53	54	55	56	57
58	59	60	61	62	63	64	65	66	67	68	69	70	71
72	73	74	75	76	77	78	79	80	81	82	83	84	85
86	87	88	89	90	91	92	93	94	95	96	97	98	99

2	3	.	5	.	7	.	9	.	11	.	13	.	15
.	17	.	19	.	21	.	23	.	25	.	27	.	29
.	31	.	33	.	35	.	37	.	39	.	41	.	43
.	45	.	47	.	49	.	51	.	53	.	55	.	57
.	59	.	61	.	63	.	65	.	67	.	69	.	71
.	73	.	75	.	77	.	79	.	81	.	83	.	85
.	87	.	89	.	91	.	93	.	95	.	97	.	99
.	101	.	103	.	104	.	107	.	109	.	111	.	113

2	3	.	5	.	7	.	.	.	11	.	13	.	.
.	17	.	19	.	.	.	23	.	25	.	.	.	29
.	31	.	.	.	35	.	37	.	.	.	41	.	43
.	.	.	47	.	49	.	.	.	53	.	55	.	.
.	59	.	61	.	.	.	65	.	67	.	.	.	71
.	73	.	.	.	77	.	79	.	.	.	83	.	85
.	.	.	89	.	91	.	.	.	95	.	97	.	.
.	101	.	103	.	.	.	107	.	109	.	.	.	113

2	3	.	5	.	7	.	.	.	11	.	13	.	.
.	17	.	19	.	.	.	23	.	.	.	.	.	29
.	31	.	.	.	.	.	37	.	.	.	41	.	43
.	.	.	47	.	49	.	.	.	53	.	.	.	.
.	59	.	61	.	.	.	.	.	67	.	.	.	71
.	73	.	.	.	77	.	79	.	.	.	83	.	.
.	.	.	89	.	91	.	.	.	.	.	97	.	.
.	101	.	103	.	.	.	107	.	109	.	.	.	113

ترجمه‌های کامران بزرگزاد

show_banner(0);

دغدغه اعداد اول

جان داربی‌شِر

ترجمه کامران بزرگزاد ایمانی

مقدمه مترجم

درباره این کتاب

کتاب مورد استفاده چه کسانی است

درباره نویسنده

مقدمه مؤلف

فصل 1

ترفند ورق‌های بازی

1.

2.

3.

4.

5.

6.

7.

8.

فصل 2

خاک و محصول

1.

2.

3.

4.

5.

6.

7.

فصل 3

قضیه اعداد اول

1.

2.

فصل 4

بر روی شانه غول‌ها

1.

2.

فصل 5

تابع زتای ریمان

1.

2.

فصل 6

هم‌آمیزی بزرگ

1.

2.

3.

فصل 7

کلید طلایی، و یک قضیه اعداد اولِ بهبود یافته

1.

2.

3.

فصل 8

تلاشهای نه چندان بی‌ارزش

1.

2.

3.

فصل 9

گسترش دامنه

1.

2.

فصل 10

یک اثبات و یک نقطه عطف

1.

2.

3.

فصل 11

دستگاه‌های مختلف اعداد

1.

2.

فصل 12

مسئله هشتم هیلبرت

1.

2.

فصل 13

نمودارهای آرگومانی و مقداری

1.

فصل 14

اولین دغدغه‌ها

1.

2.

2	3	4	5	6	7	8	9	10	11	12	13	14	15
16	17	18	19	20	21	22	23	24	25	26	27	28	29
30	31	32	33	34	35	36	37	38	39	40	41	42	43
44	45	46	47	48	49	50	51	52	53	54	55	56	57
58	59	60	61	62	63	64	65	66	67	68	69	70	71
72	73	74	75	76	77	78	79	80	81	82	83	84	85
86	87	88	89	90	91	92	93	94	95	96	97	98	99

2	3	.	5	.	7	.	9	.	11	.	13	.	15
.	17	.	19	.	21	.	23	.	25	.	27	.	29
.	31	.	33	.	35	.	37	.	39	.	41	.	43
.	45	.	47	.	49	.	51	.	53	.	55	.	57
.	59	.	61	.	63	.	65	.	67	.	69	.	71
.	73	.	75	.	77	.	79	.	81	.	83	.	85
.	87	.	89	.	91	.	93	.	95	.	97	.	99
.	101	.	103	.	104	.	107	.	109	.	111	.	113

2	3	.	5	.	7	.	.	.	11	.	13	.	.
.	17	.	19	.	.	.	23	.	25	.	.	.	29
.	31	.	.	.	35	.	37	.	.	.	41	.	43
.	.	.	47	.	49	.	.	.	53	.	55	.	.
.	59	.	61	.	.	.	65	.	67	.	.	.	71
.	73	.	.	.	77	.	79	.	.	.	83	.	85
.	.	.	89	.	91	.	.	.	95	.	97	.	.
.	101	.	103	.	.	.	107	.	109	.	.	.	113

2	3	.	5	.	7	.	.	.	11	.	13	.	.
.	17	.	19	.	.	.	23	.	.	.	.	.	29
.	31	.	.	.	.	.	37	.	.	.	41	.	43
.	.	.	47	.	49	.	.	.	53	.	.	.	.
.	59	.	61	.	.	.	.	.	67	.	.	.	71
.	73	.	.	.	77	.	79	.	.	.	83	.	.
.	.	.	89	.	91	.	.	.	.	.	97	.	.
.	101	.	103	.	.	.	107	.	109	.	.	.	113